某医疗研究所为了检验新开发的流感疫苗对甲型H1N1流感的预防作用,把1000名注射了疫苗的人与另外1000名未注射疫苗的人的半年的感冒记录作比较,提出假设H0:“这种疫苗不能起到预防甲型H1N1流感的作用”,经计算得到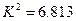 ,且
,且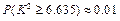 ,则下列说法正确的是( )
,则下列说法正确的是( )
| A.这种疫苗能起到预防甲型H1N1流感的有效率为1% |
| B.若某人未使用该疫苗,则他在半年中有99%的可能性得甲型H1N1 |
| C.有1%的把握认为“这种疫苗能起到预防甲型H1N1流感的作用” |
| D.有99%的把握认为“这种疫苗能起到预防甲型H1N1流感的作用. |
(本小题满分12分)
在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人。女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动。
(1)根据以上数据建立一个2×2列联表;
(2)判断休闲方式与性别是否有关。
(参考公式:
参考数据: )
)
为研究变量 的线性相关性,甲、乙二人分别作了研究,利回线性回归方法
的线性相关性,甲、乙二人分别作了研究,利回线性回归方法
得到回归直线方程 ,两人计算知
,两人计算知 相同,
相同, 也相同,下列正确的是( )
也相同,下列正确的是( )
A. 重合 重合 |
B. 一定平行 一定平行 |
C. |
D.无法判断 是否相交 是否相交 |
(本小题满分12分)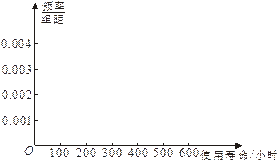
对某电子元件进行寿命追踪调查,情况如下:
| 寿命/小时 |
100~200 |
200~300 |
300~400 |
400~500 |
500~600 |
| 个数 |
20 |
30 |
80 |
40 |
30 |
(1)完成频率分布表;
| 分组 |
频数 |
频率 |
| 100~200 |
|
|
| 200~300 |
|
|
| 300~400 |
|
|
| 400~500 |
|
|
| 500~600 |
|
|
| 合计 |
|
|
(2)画出频率分布直方图和频率分布折线图;
(3)估计电子元件寿命在100~400小时以内的频率;
假设关于某设 备的使用年限
备的使用年限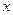 (年)和所支出的维修费用
(年)和所支出的维修费用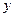 (万元)有如下统计资料:
(万元)有如下统计资料:
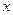 (年) (年) |
2 |
3 |
4 |
5 |
6 |
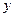 (万元) (万元) |
2.2 |
3.8 |
5.5 |
6.5 |
7.0 |
若由资料知,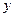 对
对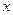 呈线性相关关系,且有如下参考数据:
呈线性相关关系,且有如下参考数据: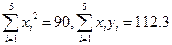 ,则回归直线方程为
,则回归直线方程为
A. |
B.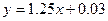 |
C.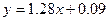 |
D.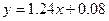 |
设三组实验数据(x1,y1),(x2,y2),(x3,y3)的回归直线方程是: =
= x+
x+ ,使代数式[y1-(
,使代数式[y1-( x1+
x1+ )]2+[y2-(
)]2+[y2-( x2+
x2+ )]2+[y3-(
)]2+[y3-( x3+
x3+ )]2的值最小时,
)]2的值最小时, =
= -
-
 ,
, =
=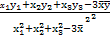 (
( ,
, 分别是这三组数据的横、纵坐标的平均数),
分别是这三组数据的横、纵坐标的平均数),
若有7组数据列表如下:
| x |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| y |
4 |
6 |
5 |
6.2 |
8 |
7.1 |
8.6 |
(1)求上表中前3组数据的回归直线方程.
(2)若|yi-( xi+
xi+ )|≤0.2,即称(xi,yi)为(1)中回归直线的拟合“好点”,求后4组数据中拟合“好点”的概率.
)|≤0.2,即称(xi,yi)为(1)中回归直线的拟合“好点”,求后4组数据中拟合“好点”的概率.
为了解高二某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表: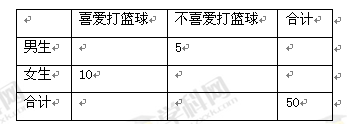
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为 .
.
(1)请将上面的列联表补充完整;
(2)是否有99.5%的把握认为喜爱打篮球与性别有关?说明你的理由;
下面的临界值表供参考:
(参考公式K2= ,其中n=a+b+c+d)
,其中n=a+b+c+d)
(满分12分)假设关于某设备的使用年限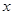 和所支出的维修费用
和所支出的维修费用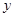 (万元)有如下的统计资料:
(万元)有如下的统计资料:
使用年限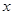 |
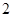 |
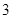 |
 |
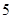 |
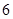 |
维修费用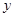 |
 |
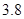 |
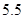 |
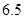 |
 |
若由资料知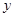 对
对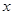 呈线性相关关系。
呈线性相关关系。
(1)请画出上表数据的散点图;
(2)请根据最小二乘法求出线性回归方程 的回归系数
的回归系数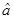 ,
,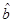 .
.
(3)估计使用年限为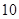 年时,维修费用是多少?
年时,维修费用是多少?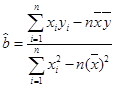 ,
,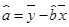
由某种设备的使用年限 (年)与所支出的维修费
(年)与所支出的维修费 (万元)的数据资料,算得
(万元)的数据资料,算得 ,
, ,
, ,
,  .
.
(Ⅰ)求所支出的维修费 对使用年限
对使用年限 的线性回归方程
的线性回归方程 ;
;
(Ⅱ)判断变量 与
与 之间是正相关还是负相关;
之间是正相关还是负相关;
(Ⅲ)估计使用年限为8年时,支出的维修费约是多少.
附:在线性回归方程 中,
中, ,
, ,其中
,其中 ,
, 为
为
样本平均值,线性回归方程也可写为 .
.
为了预防甲型H1N1流感,某学校对教室用药薰消毒法进行消毒,已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与t时间(小时)成正比,药物释放完毕后,y与t之间的函数关系式为 (a为常数)如下图所示,根据图中提供的信息,回答下列问题.
(a为常数)如下图所示,根据图中提供的信息,回答下列问题.
(1)从药物释放开始,求每立方米空气中的含药量y(毫克)与时间t(小时)之间的函数关系式;
(2)据测定,当空气中每立方米的含药量降低到0.25毫克以下时,学生方可进教室,那么从药物释放开始至少需要经过多少小时后,学生才可能回到教室.
在2010年3月15日那天,龙岩市物价部门对本市5家商场某商品的一天销售量及其价格进行调查,5家商场的售价 元和销售量
元和销售量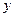 件之间的一组数据如右表所示,由散点图可知,销售量y与价格
件之间的一组数据如右表所示,由散点图可知,销售量y与价格 之间有较好的线性相关关系,若其线性回归直线方程是:
之间有较好的线性相关关系,若其线性回归直线方程是: ,(参考公式:回归方程;
,(参考公式:回归方程; ),则
),则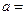 ___________。
___________。
价格 |
9 |
9.5 |
10 |
10.5 |
11 |
销售量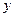 |
11 |
10 |
8 |
6 |
5 |
下列四个命题正确的是 ( )
①线性相关系数r越大,两个变量的线性相关性越强;反之,线性相关性越小;
②残差平方和越小的模型,拟合的效果越好;
③用相关指数R2来刻画回归效果,R2越小,说明模型的拟合效果越好。
④随机误差e是衡量预报精确度的一个量,它满足E(e)=0
| A.①③ | B.②④ | C.①④ | D.②③ |
.以下是粤西地区某县搜集到的新房屋的销售价格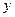 和
和 房屋的面积
房屋的面积 的数据:
的数据: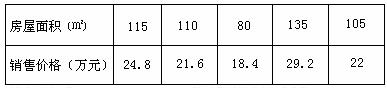
(1)画出数据散点图;
(2)由散点图判断新房屋销售价格y和房屋面积x是否具有线性相关关系?若有,求线性回 归方程。(保留四位小数)
归方程。(保留四位小数)
(3)根据房屋面积预报销售价格的回归方程,预报房屋面积为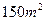 时的销售价格。
时的销售价格。
参考公式: 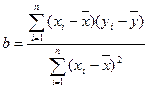 ,
,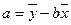
参考数据: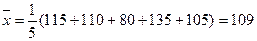 ,
,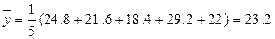
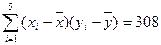 ,
,
(本小题满分12分)某地区2007年至2013年农村居民家庭纯收入 (单位:千元)的数据如下表:
(单位:千元)的数据如下表:
| 年份 |
2007 |
2008 |
2009 |
2010 |
2011 |
2012 |
2013 |
年份代号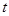 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
人均纯收入 |
2.9 |
3.3 |
3.6 |
4.4 |
4.8 |
5.2 |
5.9 |
(Ⅰ)求 关于
关于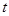 的线性回归方程;(已知b=0.5)
的线性回归方程;(已知b=0.5)
(Ⅱ)利用(Ⅰ)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
试题篮
()