某班有60名学生,一次考试后数学成绩 ,若
,若 ,则估计该班学生数学成绩在120分以上的人数为( )
,则估计该班学生数学成绩在120分以上的人数为( )
| A.10 | B.9 | C.8 | D.7 |
[2014·抚顺模拟]已知随机变量ξ服从正态分布N(0,σ2),若P(ξ>2)=0.023,则P(-2≤ξ≤2)=( )
| A.0.477 | B.0.628 | C.0.954 | D.0.977 |
设随机变量X~N(2,32),若P(X≤c)=P(X>c),则c等于( )
| A.0 | B.1 | C.2 | D.3 |
已知随机变量
服从正态分布
,且
,则
()
| A. | 0.6 | B. | 0.4 | C. | 0.3 | D. | 0.2 |
已知随机变量X服从正态分布N(3.1),且 =0.6826,则p(X>4)=( )
=0.6826,则p(X>4)=( )
| A.0.1588 | B.0.1587 | C.0.1586 | D.0.1585 |
假设每天从甲地去乙地的旅客人数X是服从正态分布N(800,502)的随机变量,则一天中从甲地去乙地的旅客人数不超过900的概率P0=( )
(参考数据:若X~N(μ,σ2),有P(μ-σ<X≤μ+σ)=0.6826,P(μ-2σ<X≤μ+2σ)=0.9544,
P(μ-3σ<X≤μ+3σ)=0.9974.)
| A.0.954 | B.0.9974 | C.0.9772 | D.0.9773 |
已知随机变量 服从正态分布N(2,σ2),且P(
服从正态分布N(2,σ2),且P( <4)=0.8,则P(0<
<4)=0.8,则P(0< <2)=( )
<2)=( )
| A.0.6 | B.0.4 | C.0.3 | D.0.2 |
已知随机变量ξ服从正态分布N(0,σ2).若P(ξ>2)=0.023,则P(-2≤ξ≤2)=( )
| A.0.954 | B.0.046 | C.0.977 | D.0.846 |
节日前夕,小李在家门前的树上挂了两串彩灯.这两串彩灯的第一次闪亮相互独立,且都在通电后的4秒内任一时刻等可能发生,然后每串彩灯以4秒为间隔闪亮.那么这两串彩灯同时通电后,它们第一次闪亮的时刻相差不超过2秒的概率是( )
A. |
B. |
C. |
D. |
从1,2,3,4,5中任取2个不同的数,事件A=“取到的2个数之和为偶数”,事件B=“取到的2个数均为偶数”,则P(B|A)=( )
A. B.
B. C.
C. D.
D.
以下四个命题中:
①从匀速传递的产品生产流水线上,质检员每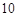 分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样;
分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样;
②若两个变量的线性相关性越强,则相关系数的绝对值越接近于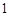 ;
;
③在某项测量中,测量结果 服从正态分布
服从正态分布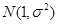
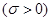 ,若
,若 位于区域
位于区域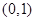 内的概率为
内的概率为 ,则
,则 位于区域
位于区域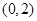 内的概率为
内的概率为 ;
;
④对分类变量 与
与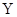 的随机变量K2的观测值k来说,k越小,判断“
的随机变量K2的观测值k来说,k越小,判断“ 与
与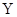 有关系”的把握越大.其中真命题的序号为( )
有关系”的把握越大.其中真命题的序号为( )
| A.①④ | B.②④ | C.①③ | D.②③ |
以下四个命题中:
①从匀速传递的产品生产流水线上,质检员每10分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样;
②两个随机变量的线性相关性越强,相关系数的绝对值越接近于1;
③在某项测量中,测量结果ξ服从正态分布N(1,σ2)(σ>0),若ξ在(0,1)内取值的概率为0.4,则ξ在(0,2)内取值的概率为0.8 ;
④对分类变量X与Y的随机变量k2的观测值k来说,k越小,判断“X与Y有关系”的把握程度越大.
其中真命题的个数为( )
| A.4 | B.3 | C.2 | D.1 |
以下四个命题中:
①为了了解800名学生对学校某项教改试验的意见,打算从中抽取一个容量为 的样本,考虑用系统抽样,则分段的间隔
的样本,考虑用系统抽样,则分段的间隔 为40.
为40.
②线性回归直线方程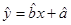 恒过样本中心
恒过样本中心 ,且至少过一个样本点;
,且至少过一个样本点;
③在某项测量中,测量结果ξ服从正态分布 .若ξ在
.若ξ在 内取值的概率为
内取值的概率为 ,则ξ在
,则ξ在 内取值的概率为
内取值的概率为 ;
;
其中真命题的个数为( )
A. |
B. |
C. |
D. |
试题篮
()