顺义二中对文明班的评选设计了 五个方面的多元评价指标,并通过经验公式
五个方面的多元评价指标,并通过经验公式 来计算各班的综合得分,
来计算各班的综合得分, 的值越高则评价效果越好.若某班在自测过程中各项指标显示出
的值越高则评价效果越好.若某班在自测过程中各项指标显示出 ,则下阶段要把其中一个指标的值增加
,则下阶段要把其中一个指标的值增加 个单位,而使得
个单位,而使得 的值增加最多,那么该指标应为 .(填入
的值增加最多,那么该指标应为 .(填入 中的某个字母)
中的某个字母)
由①正方形的四个内角相等;②矩形的四个内角相等;③正方形是矩形,根据“三段论”推理得出一个结论,则作为大前提、小前提、结论的分别为( )
| A.②①③ | B.③①② | C.①②③ | D.②③① |
类比平面内 “垂直于同一条直线的两条直线互相平行”的性质,可推出空间下列结论:①垂直于同一条直线的两条直线互相平行;②垂直于同一个平面的两条直线互相平行;③垂直于同一条直线的两个平面互相平行;④垂直于同一个平面的两个平面互相平行.则正确结论的序号是
正弦函数是奇函数,f(x)=sin(x2+1)是正弦函数,因此f(x)=sin(x2+1)是奇函数.以上推理( )
| A.结论正确 |
| B.大前提不正确 |
| C.小前提不正确 |
| D.全不正确 |
某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数 .
.
① ;
;
② ;
;
③ ;
;
④ ;
;
⑤ .
.
(1)从上述五个式子中选择一个,求出常数 ;
;
(2)根据(1)的计算结果,将该同学的发现推广为一个三角恒等式,并证明你的结论.
现有一个关于平面图形的命题:如图,同一个平面内有两个边长都是 的正方形,其中一个的某顶点在另一个的中心,则这两个正方形重叠部分的面积恒为
的正方形,其中一个的某顶点在另一个的中心,则这两个正方形重叠部分的面积恒为 .类比到空间,有两个棱长均为
.类比到空间,有两个棱长均为 的正方体,其中一个的某顶点在另一个的中心,则这两个正方体重叠部分的体积恒为 .
的正方体,其中一个的某顶点在另一个的中心,则这两个正方体重叠部分的体积恒为 . 
在平面几何里,有勾股定理:“设 的两边AB、AC互相垂直,则
的两边AB、AC互相垂直,则 。”拓展到空间,类比平面几何的勾股定理,研究三棱锥的侧面积与底面积间的关系,可以得到的正确结论是:“设三棱锥A-BCD的三个侧面ABC 、ACD、ADB两两互相垂直,则 ”。
。”拓展到空间,类比平面几何的勾股定理,研究三棱锥的侧面积与底面积间的关系,可以得到的正确结论是:“设三棱锥A-BCD的三个侧面ABC 、ACD、ADB两两互相垂直,则 ”。
下面几种推理过程是演绎推理的是 ( )
A.两条直线平行,同旁内角互补,如果 和 和 是两条平行直线的同旁内角,则 是两条平行直线的同旁内角,则 . . |
| B.由平面三角形的性质,推测空间四面体性质. |
| C.某校高二共有10个班,1班有51人,2班有53人,3班有52人,由此推测各班都超过50人. |
D.在数列 中 中 ,由此归纳出 ,由此归纳出 的通项公式. 的通项公式. |
已知幂函数 是增函数,而
是增函数,而 是幂函数,所以
是幂函数,所以 是增函数,上面推理错误是( )
是增函数,上面推理错误是( )
| A.大前提错误导致结论错 | B.小前提错误导致结论错 |
| C.推理的方式错误导致错 | D.大前提与小前提都错误导致错 |
n个连续自然数按规律排成下表:
0 3 → 4 7 → 8 11 …
↓ ↑ ↓ ↑ ↓ ↑
1 → 2 5 → 6 9 → 10
根据规律,从2 009到2 011的箭头方向依次为________.
①↓→ ②→↑ ③↑→ ④→↓
有一段“三段论”推理是这样的:对于可导函数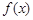 ,如果
,如果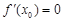 ,那么
,那么 是函数
是函数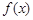 的极值点,因为函数
的极值点,因为函数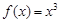 在
在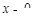 处的导数值
处的导数值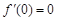 ,所以,
,所以,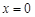 是函数
是函数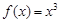 的极值点.以上推理中( )
的极值点.以上推理中( )
| A.大前提错误 | B.小前提错误 | C.推理形式错误 | D.结论正确 |
试题篮
()