高中数学合情推理和演绎推理试题

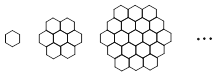
蜜蜂被认为是自然界中最杰出的建筑师，单个蜂巢可以近似地看作是一个正六边形，如图为一组蜂
巢的截面图. 其中第一个图有1个蜂巢，第二个图有7个蜂巢，第三个图有19个蜂巢，按此规律，
以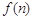表示第幅图的蜂巢总数，则=_______.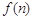

设ΔABC的三边长分别为、、，ΔABC的面积为，则ΔABC的内切圆半径为，
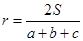将此结论类比到空间四面体：设四面体S—ABCD的四个面的面积分别为，，，，
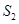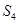体积为，则四面体的内切球半径=           ．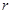

椭圆的标准方程为（），圆的标准方程，即，类比圆的面积推理得椭圆的面积         。

设等差数列的前项和为，则,,,
成等差数列.类比以上结论有：设等比数列的前项积为，则成等比数列.

观察下图：
1
2　3　4
3　4　5　6　7
4　5　6　7　8　9　10
……
则第________行的各数之和等于2 013²                                                  (　　)．

A．2 014

B．2 013

C．1 007

D．1 008

①由“若a，b，c∈R，则(ab)c＝a(bc)”类比“若a、b、c为三个向量，则(a·b)c＝a(b·c)”；
②在数列{a_n}中，a₁＝0，a_n＋1＝2a_n＋2，猜想a_n＝2ⁿ－2；
③在平面内“三角形的两边之和大于第三边”类比在空间中“四面体的任意三个面的面积之和大于第四个面的面积”；
上述三个推理中，正确的个数为(　　)

A．0

B．1

C．2

D．3

观察下列不等式



……
照此规律，第五个不等式为________．

把正整数按右图所示的规律排序，则从2013到2015的箭头方向依次为（　　）

A．

B．

C．

D．

推理：因为平行四边形对边平行且相等，而矩形是特殊的平行四边形，所以矩形的对边平行且相等．以上推理的方法是（   ）

A．合情推理

B．演绎推理

C．归纳推理

D．类比推理

法国数学家费马观察到，，，都是质数，于是他提出猜想：任何形如N*）的数都是质数，这就是著名的费马猜想. 半个世纪之后，善于发现的欧拉发现第5个费马数不是质数，从而推翻了费马猜想，这一案例说明( )

A．归纳推理，结果一定不正确	B．归纳推理，结果不一定正确
C．类比推理，结果一定不正确	D．类比推理，结果不一定正确

蜜蜂被认为是自然界中最杰出的建筑师，单个蜂巢可以近似地看作是一个正六边形，如图为
一组蜂巢的截面图．其中第一个图有1个蜂巢，第二个图有7个蜂巢，第三个图有19个蜂巢，
按此规律，以表示第幅图的蜂巢总数.则
=_____，=___________．

（设数列的前项和为，且满足．
（1）求，，，的值并写出其通项公式；
（2）用三段论证明数列是等比数列．

如图所示的三角形数组是我国古代数学家杨辉发现的，称为杨辉三角形，根据图中的数构成的规律，所表示的数是

A．2

B．4

C．6

D．8

用火柴棒摆“金鱼”，如图所示：

按照上面的规律，第4个“金鱼”图需要火柴棒的根数为

A．24

B．26

C．28

D．30

已知椭圆具有性质：若是椭圆：且为常数上关于原点对称的两点，点是椭圆上的任意一点，若直线和的斜率都存在，并分别记为，，那么．类比双曲线且为常数中，若是双曲线且为常数上关于原点对称的两点，点是双曲线上的任意一点，若直线和的斜率都存在，并分别记为，，那么      ．