高中数学合情推理和演绎推理试题

两千多年前，古希腊毕达哥拉斯学派的数学家曾经在沙滩上研究数学问题，他们在沙滩上画点或用小石子来表示数，按照点或小石子能排列的形状对数进行分类，图中的实心点的个数1、5、12、22、…，被称为五角形数，其中第1个五角形数记作，第2个五角形数记作，第3个五角形数记作
，第4个五角形数记作，……，若按此规律继续下去，则____，若，则
＝______.

黑白两种颜色的正六边形地面砖按如图的规律拼成若干个图案：

则第n个图案中有白色地面砖                块．

已知若均为正实数)，则类比以上等式，可推测a、b的值，进而可得a＋b＝     .

如图，在单位圆中，用三角形的重心公式研究内接正三角形（点在轴上），有结论：。有位同学，把正三角形按逆时针方向旋转角，这时，可以得到一个怎样的结论呢？答：                             。

“π是无限不循环小数，所以π是无理数”，以上推理（ ）

A．缺少小前提，小前提是无理数都是无限不循环小数

B．缺少大前提，大前提是无理数都是无限不循环小数

C．缺少小前提，小前提是无限不循环小数都是无理数

D．缺少大前提，大前提是无限不循环小数都是无理数

下列表述正确的是（ ）
①归纳推理是由特殊到一般的推理；
②演绎推理是由一般到特殊的推理；
③类比推理是由特殊到一般的推理；
④分析法是一种间接证明法；
⑤若z∈C，且|z+2﹣2i|=1，则|z﹣2﹣2i|的最小值是3．

A．①②③④

B．②③④

C．①②④⑤

D．①②⑤

观察下列等式:
,
,
,
,

由以上等式推测:
对于,若,则          .

集合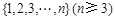中，每两个相异数作乘积，将所有这些乘积的和记为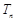，如：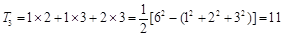
；
；

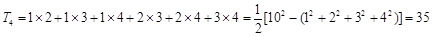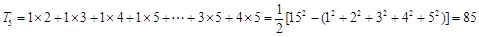
则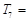          ．（写出计算结果）

将全体正整数排成一个三角形数阵：

按照以上排列的规律，第行从左向右的第3个数为           

依此类推，第个等式为                    ．

观察下列式子：根据以上式子可以猜想：

A．

B．

C．

D．

设等差数列的前n项和为则成等差数列.类比以上结论有:设等比数列的前n项积为则         ，           ，成等比数列．

由下列事实：
（a﹣b）（a+b）=a²﹣b²
（a﹣b）（a²+ab+b²）=a³﹣b³，
（a﹣b）（a³+a²b+ab²+b³）=a⁴﹣b⁴，
（a﹣b）（a⁴+a³b+a²b²+ab³+b⁴）=a⁵﹣b⁵，
可得到合理的猜想是               ．

定义表示所有满足的集合组成的有序集合对的个数．试探究，并归纳推得=_________.

在平面中，△ABC的角C的内角平分线CE分△ABC面积所成的比.将这个结论类比到空间：在三棱锥A－BCD中，平面DEC平分二面角A－CD－B且与AB交于E，则类比的结论为＝________．