对大于或等于2的自然数m的n次方幂有如下分解方式:
22=1+3 23=3+5
32=1+3+5 33=7+9+11
42=1+3+5+7 43=13+15+17+19
52=1+3+5+7+9 53=21+23+25+27+29
根据上述分解规律,若m3(m∈N*)的分解中最小的数是73,则m的值为________.
观察下列各式:a+b=1,a2+b2=3,a3+b3=4,a4+b4=7,a5+b5=11,…,则a10+b10=( )
| A.28 | B.76 | C.123 | D.199 |
已知正三角形内切圆的半径 与它的高
与它的高 的关系是:
的关系是: ,把这个结论推广到空间正四面体,则正四面体内切球的半径
,把这个结论推广到空间正四面体,则正四面体内切球的半径 与正四面体高
与正四面体高 的关系是 .
的关系是 .
对于问题:“已知关于 的不等式
的不等式 的解集为(-1,2),解关于
的解集为(-1,2),解关于 的不等式
的不等式 ”,给出如下一种解法:
”,给出如下一种解法:
解:由 的解集为(-1,2),得
的解集为(-1,2),得 的解集为(-2,1),
的解集为(-2,1),
即关于 的不等式
的不等式 的解集为(-2,1)
的解集为(-2,1)
参考上述解法,若关于 的不等式
的不等式 的解集为(-1,
的解集为(-1,  )
) (
( ,1),则关于
,1),则关于 的不等式
的不等式 的解集为________________
的解集为________________
将长度为 的线段分成
的线段分成 段,每段长度均为正整数,并要求这
段,每段长度均为正整数,并要求这 段中的任意三段都不能构成三角形.例如,当
段中的任意三段都不能构成三角形.例如,当 时,只可以分为长度分别为1,1,2的三段,此时
时,只可以分为长度分别为1,1,2的三段,此时 的最大值为3;当
的最大值为3;当 时,可以分为长度分别为1,2,4的三段或长度分别为1,1,2,3的四段,此时
时,可以分为长度分别为1,2,4的三段或长度分别为1,1,2,3的四段,此时 的最大值为4.则:
的最大值为4.则:
(1)当 时,
时, 的最大值为________;
的最大值为________;
(2)当 时,
时, 的最大值为________.
的最大值为________.
将长度为 的线段分成
的线段分成 段,每段长度均为正整数,并要求这
段,每段长度均为正整数,并要求这 段中的任意三段都不能构成三角形.例如,当
段中的任意三段都不能构成三角形.例如,当 时,只可以分为长度分别为1,1,2的三段,此时
时,只可以分为长度分别为1,1,2的三段,此时 的最大值为3;当
的最大值为3;当 时,可以分为长度分别为1,2,4的三段或长度分别为1,1,2,3的四段,此时
时,可以分为长度分别为1,2,4的三段或长度分别为1,1,2,3的四段,此时 的最大值为4.则:
的最大值为4.则:
(1)当 时,
时, 的最大值为________;(2)当
的最大值为________;(2)当 时,
时, 的最大值为________.
的最大值为________.
已知集合A={3m+2n|m>n且m,n∈N},若将集合A中的数按从小到大排成数列{an},则有a1=31+2×0=3,a2=32+2×0=9,a3=32+2×1=11,a4=33=27,…,依此类推,将数列依次排成如图所示的三角形数阵,则第六行第三个数为( )
| A.247 | B.735 |
| C.733 | D.731 |
由“正三角形的内切圆切于三边的中点”可类比猜想:正四面体的内切球切于四个面( )
| A.各正三角形内一点 | B.各正三角形的某高线上的点 |
| C.各正三角形的中心 | D.各正三角形外的某点 |
有一个奇数列1, 3, 5, 7, 9,…,现在进行如下分组:第一组含一个数 ,第二组含两个数
,第二组含两个数 ,第三组含三个数
,第三组含三个数 ,第四组含四个数
,第四组含四个数 ,…,现观察猜想每组内各数之和为
,…,现观察猜想每组内各数之和为 与其组的编号数
与其组的编号数 的关系为 .
的关系为 .
在计算“1×2+2×3+...+n(n+1)”时,某同学学到了如下一种方法:
先改写第k项:k(k+1)=
由此得1×2- .
. .
.
............. .
.
相加,得1×2+2×3+...+n(n+1) .
.
类比上述方法,请你计算“1×2×3×4+2×3×4×+....+ ”,
”,
其结果是_________________.(结果写出关于 的一次因式的积的形式)
的一次因式的积的形式)
在计算“1×2+2×3+...+n(n+1)”时,某同学学到了如下一种方法:
先改写第k项:k(k+1)=
由此得1×2= .
. .
.
............. .
.
相加,得1×2+2×3+...+n(n+1) .
.
类比上述方法,请你计算“1×2×3×4+2×3×4×+....+ ”,其结果是_________________.(结果写出关于
”,其结果是_________________.(结果写出关于 的一次因式的积的形式)
的一次因式的积的形式)
定义函数 ,其中
,其中 表示不小于
表示不小于 的最小整数,如
的最小整数,如 ,
, .当
.当 (
(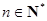 )时,函数
)时,函数 的值域为
的值域为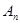 ,记集合
,记集合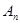 中元素的个数为
中元素的个数为 ,则
,则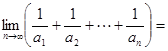 ________________.
________________.
试题篮
()