“因为指数函数y=ax是增函数,而y= 是指数函数,所以y=
是指数函数,所以y= 是增函数”,上面推理的错误是( )
是增函数”,上面推理的错误是( )
| A.大前提错导致结论错; | B.小前提错导致结论错; |
| C.推理形式错导致结论错; | D.大前提和小前提错都导致结论错。 |
对“a,b,c是不全相等的正数”,给出如下判断:
①(a-b)2+(b-c)2+(c-a)2≠0;②a>b与a<b及a=b中至少有一个成立;
③a≠c,b≠c,a≠b不能同时成立,其中判断正确的个数是( )
| A.0 | B.1 | C.2 | D.3 |
锐角三角形的面积等于底乘高的一半;
直角三角形的面积等于底乘高的一半;
钝角三角形的面积等于底乘高的一半;
所以,凡是三角形的面积都等于底乘高的一半.
以上推理运用的推理规则是( )
| A.三段论推理 | B.假言推理 | C.关系推理 | D.完全归纳推理 |
观察下列各式: . , , , ,则 ()
| A. | 28 | B. | 76 | C. | 123 | D. | 199 |
有一段演绎推理是这样的:“三角函数是周期函数, 是三角函数,所以
是三角函数,所以 是周期函数.”在以上演绎推理中,下列说法正确的是( )
是周期函数.”在以上演绎推理中,下列说法正确的是( )
| A.推理完全正确 | B.大前提不正确 |
| C.小前提不正确 | D.推理形式不正确 |
有一段“三段论”推理是这样的:对于可导函数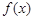 ,如果
,如果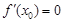 ,那么
,那么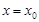 是函数
是函数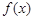 的极值点,因为函数
的极值点,因为函数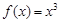 在
在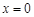 处的导数值
处的导数值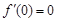 ,所以,
,所以,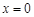 是函数
是函数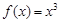 的极值点.以上推理中
的极值点.以上推理中
| A.大前提错误 | B.小前提错误 |
| C.推理形式错误 | D.结论正确 |
已知结论:“在正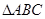 中,
中,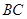 中点为
中点为 ,若
,若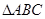 内一点
内一点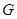 到各边的距离都相等,则
到各边的距离都相等,则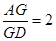 ”.若把该结论推广到空间,则有结论:“在棱长都相等的四面体
”.若把该结论推广到空间,则有结论:“在棱长都相等的四面体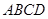 中,若
中,若 的中心为
的中心为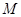 ,四面体内部一点
,四面体内部一点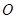 到四面体各面的距离都相等,则
到四面体各面的距离都相等,则 ( ▲ )
( ▲ )
| A.1 | B.2 | C.3 | D.4 |
下列推理是归纳推理的是( )
| A.A,B为定点,动点P满足|PA|+|PB|=2a>|AB|,得P的轨迹为椭圆 |
| B.由a1=1,an=3n-1(n>1),求出S1,S2,S3,猜想数列的前n项和Sn的表达式 |
C.由圆x2+y2=r2的面积πr2,猜出椭圆 + + =1的面积S=πab =1的面积S=πab |
| D.科学家利用鱼的沉浮原理制造潜艇 |
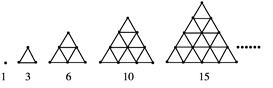
如图,把1,3,6,10,15,…这些数叫做三角形数,这是因为这些数目的点可以排成一个正三角形,则第七个三角形数是
| A.27 | B.28 | C.29 | D.30 |
有一段演绎推理是这样的:“直线平行于平面,则平行于平面内所有直线;已知直线 平面
平面 ,直线
,直线 平面
平面 ,直线
,直线 ∥平面
∥平面 ,则直线
,则直线 ∥直线
∥直线 ”的结论显然是错误的,这是因为( )
”的结论显然是错误的,这是因为( )
| A.推理形式错误 | B.小前提错误 | C.大前提错误 | D.非以上错误 |
已知三角形的三边分别为 ,内切圆的半径为
,内切圆的半径为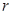 ,则三角形的面积为
,则三角形的面积为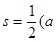
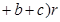 ;四面体的四个面的面积分别为
;四面体的四个面的面积分别为 ,内切球的半径为
,内切球的半径为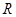 。类比三角形的面积可得四面体的体积为( )。
。类比三角形的面积可得四面体的体积为( )。
A. |
B.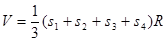 |
C. |
D.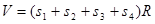 |
试题篮
()