高中数学合情推理和演绎推理选择题

“自然数是整数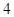，是自然数，所以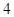是整数.”以上三段推理（    ）。

A．完全正确

B．推理形式不正确

C．不正确，因为两个“自然数”概念不一致

D．不正确，因为两个“整数”概念不一致

下面使用类比推理正确的是 （       ）.                                              

A．“若,则”类推出“若,则”

B．“若”类推出“”

C．“若” 类推出“（c≠0）”

D．“” 类推出“”

下列表述正确的是（       ）.
①归纳推理是由部分到整体的推理；②归纳推理是由一般到一般的推理；③演绎推理是由一般到特殊的推理；④类比推理是由特殊到一般的推理；⑤类比推理是由特殊到特殊的推理.

A．①②③；

B．②③④；

C．②④⑤；

D．①③⑤.

在平面几何中有如下结论：若正三角形的内切圆面积为，外接圆面积为，则，推广到空间几何中可以得到类似结论：若正四面体的内切球体积为，外接球体积为，则（   ）

A．

B．

C．

D．

将石子摆成如图的梯形形状，称数列为“梯形数”．根据图形的构成，数列的第10项为（   ）

A．

B．

C．

D．

已知，则与的关系为          （   ）

A．
B．
C．	D．

用正偶数按下表排列

	第1列	第2列	第3列	第4列	第5列
第一行		2	4	6	8
第二行	16	14	12	10
第三行		18	20	22	24
…		…	28	26

则2012在第     行第   列（   ）
A．第   251  行第  3 列          B．第   252  行第  3 列  
C．第   250  行第  4 列             D．第   251  行第  4 列

三角形的面积为为三角形的边长，r为三角形内切圆的半径，利用类比推理，可得出四面体的体积为（ ）

A．

B．

C．（分别为四面体的四个面的面积，r为四面体内切球的半径）

D．

如下图，第（1）个多边形是由正三角形“扩展“而来，第（2）个多边形是由正方形“扩展”而来，……，如此类推.设由正边形“扩展”而来的多边形的边数为，
则＝（ ）
           

A．；

B．；

C．；

D．

四个小动物换座位，开始是鼠、猴、兔、猫分别坐1，2，3，4号位子上（如图），第一
次前后排动物互换座位，第二次左右列动物互换座位，…，这样交替进行下去，那么第
2012次互换座位后，小兔的座位对应的是（   ）

 
(A)编号1；        (B) 编号2；         (C) 编号3；         (D) 编号4．

下列推理正确的是（  ）

A．把与类比，则有：；

B．把与类比，则有：；

C．把与类比，则有：；

D．把与类比，则有：

观察下列各式：=3125，=15625，=78125，…，则的末四位数字为(    )

A．3125

B．5625

C．0625

D．8125

对于……大前提
……小前提
所以……结论
以上推理过程中的错误为（   ）

A．大前提

B．小前提

C．结论

D．无错误

有一段“三段论”推理是这样的：对于可导函数，如果，那么是函数的极值点，因为函数在处的导数值，所以，是函数的极值点.以上推理中（   ）                          

A．大前提错误

B．小前提错误

C．推理形式错误

D．结论正确

下列命题中正确的是(     )

A．类比推理是一般到特殊的推理

B．演绎推理的结论一定是正确的

C．合情推理的结论一定是正确的

D．演绎推理在前提和推理形式都正确的前提下，得到的结论一定是正确的