有一段“三段论”推理是这样的:对于可导函数 ,若
,若 ,则
,则 是函数
是函数 的极值点.因为
的极值点.因为 在
在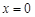 处的导数值
处的导数值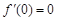 ,所以
,所以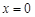 是
是 的极值点. 以上推理中
的极值点. 以上推理中
| A.大前提错误 | B.小前提错误 | C.推理形式错误 | D.结论正确 |
有一段演绎推理是这样的“有些有理数是真分数,整数是有理数,则整数是真分数”该结论显然是错误的,其原因是
| A.大前提错误 | B.小前提错误 | C.推理形式错误 | D.非以上错误 |
下列说法正确的个数是 ( )
①演绎推理是由一般到特殊的推理
②演绎推理得到的结论一定是正确的
③演绎推理的一般模式是“三段论”形式
④演绎推理得到的结论的正误与大前提、小前提和推理形式有关
| A.1 | B.2 | C.3 | D.4 |
设n为正整数,f(n)=1+ +
+ + +
+ + ,经计算得f(2)=
,经计算得f(2)= ,f(4)>2,f(8)>
,f(4)>2,f(8)>  ,f(16)>3,f(32)>
,f(16)>3,f(32)>  ,观察上述结果,可推测出一般结论( )
,观察上述结果,可推测出一般结论( )
A.f(2n)>  |
B.f(2n)≥ |
C. f(n2)≥ |
D.以上都不对 |
下列几种推理过程是演绎推理的是( )
| A.某校高三1班55人,2班54人,3班52人,由此得高三所有班级的人数超过50人 |
| B.由圆的周长C=πd推测球的表面积S=πd2 |
| C.两条直线平行,同旁内角互补,如果∠A与∠B是两条平行直线的同旁内角,则∠A+∠B=180° |
D.在数列{an}中,a1=1,an= (an﹣1+ (an﹣1+ )(n≥2),由此归纳数列{an}的通项公式 )(n≥2),由此归纳数列{an}的通项公式 |
下列说法中正确的是( )
| A.合情推理就是正确的推理 |
| B.合情推理就是归纳推理 |
| C.归纳推理是从一般到特殊的推理过程 |
| D.类比推理是从特殊到特殊的推理过程 |
如果 的三个内角的余弦值分别等于
的三个内角的余弦值分别等于 的三个内角的正弦值,则( )
的三个内角的正弦值,则( )
A. 和 和 都是锐角三角形 都是锐角三角形 |
B. 是锐角三角形, 是锐角三角形, 是钝角三角形 是钝角三角形 |
C. 是钝角三角形, 是钝角三角形, 是锐角三角形 是锐角三角形 |
D. 和 和 都是钝角三角形 都是钝角三角形 |
有一段演绎推理是这样的:“直线平行于平面,则平行于平面内所有直线;已知直线 平面
平面 ,直线
,直线 ,直线
,直线 ∥平面
∥平面 ,则直线
,则直线 ∥直线
∥直线 ”的结论显然是错误的,这是因为 ( )
”的结论显然是错误的,这是因为 ( )
| A.大前提错误 | B.小前提错误 | C.推理形式错误 | D.非以上错误 |
有一段演绎推理是这样的:“若直线平行于平面,则该直线平行于平面内所有直线;已知直线b∥平面α,直线a⊂平面α,则直线b∥直线a”,结论显然是错误的,这是因为( )
| A.大前提错误 | B.小前提错误 |
| C.推理形式错误 | D.非以上错误 |
以下说法,正确的个数为:( )
①公安人员由罪犯的脚印的尺寸估计罪犯的身高情况,所运用的是类比推理.
②农谚“瑞雪兆丰年”是通过归纳推理得到的.
③由平面几何中圆的一些性质,推测出球的某些性质这是运用的类比推理.
④个位是5的整数是5的倍数,2375的个位是5,因此2375是5的倍数,这是运用的演绎推理.
| A.0 | B.2 | C.3 | D.4 |
试题篮
()