高中数学合情推理和演绎推理解答题

在各项为正的数列{a_n}中，数列的前n项和S_n满足S_n＝.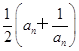
(1) 求a₁，a₂，a₃；
(2) 由(1)猜想数列{a_n}的通项公式；
(3) 求S_n.

已知 $∆ABC$的三边长为有理数
（1）求证 $\cos A$是有理数;
（2）对任意正整数 $n$,求证 $\cos nA$也是有理数.

某少数民族的刺绣有着悠久的历史，如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案，这些图案都是由小正方形构成，小正方形数越多刺绣越漂亮．现按同样的规律刺绣(小正方形的摆放规律相同)，设第n个图形包含f(n)个小正方形．

(1)求出f(5)的值；
(2)利用合情推理的“归纳推理思想”，归纳出f(n＋1)与f(n)之间的关系式，并根据你得到的关系式求出f(n)的表达式；
(3)求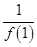＋＋＋…＋的值．

若函数满足：集合中至少存在三个不同的数构成等比数列，则称函数是等比源函数.
（1）判断下列函数：①；②中，哪些是等比源函数？（不需证明）
（2）证明：对任意的正奇数，函数不是等比源函数；
（3）证明：任意的，函数都是等比源函数.

求所有的素数对（p，q），使得．

一种十字绣作品由相同的小正方形构成，图①，②，③，④分别是制作该作品前四步时对应的图案，按照如此规律，第步完成时对应图案中所包含小正方形的个数记为．

①       ②         ③            ④
（1）求出，，，的值；
（2）利用归纳推理，归纳出与的关系式；
（3）猜想的表达式，并写出推导过程．

如图所示,底面为平行四边形ABCD的四棱锥P-ABCD中,E为PC的中点.求证:PA∥平面BDE.(要求注明每一步推理的大前提、小前提和结论,并最终把推理过程用简略的形式表示出来)

（本小题满分16分）图（1）、（2）、（3）、（4）分别包含1个、5个、13个、25个第二十九届北京奥运会吉祥物“福娃迎迎”，按同样的方式构造图形，设第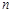个图形包含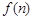个“福娃迎迎”．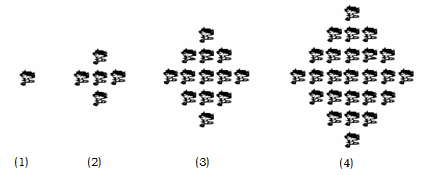

（1）求出；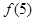
（2）利用合情推理的“归纳推理思想”归纳出与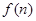的关系式（不需写出证明过程）；
（3）根据你得到的关系式求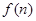的表达式．

在平面几何中，我们学习了这样一个命题：过三角形的内心作一直线，将三角形分成的两部分的周长比等于其面积比。请你类比写出在立体几何中，有关四面体的相似性质，并证之。

在锐角三角形ABC中，求证：sinA＋sinB＋sinC>cosA＋cosB＋cosC.

（本小题满分10分）
（Ⅰ）证明：．
（Ⅱ）已知圆的方程是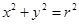，则经过圆上一点的切线方程为：
，类比上述性质，试写出椭圆类似的性质．

给定整数，证明：存在n个互不相同的正整数组成的集合S，使得对S的任意两个不同的非空子集A，B，数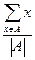
 与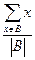 
是互素的合数．（这里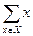与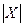分别表示有限数集的所有元素之和及元素个数．）

在中，三个内角A、B、C的对边分别为a,b,c，且A、B、C成等差数列，a,b,c成等比数列，请用分析法证明：为等边三角形。

设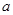是一个自然数，是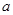的各位数字的平方和，定义数列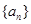：是自然数，（，）．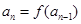
（1）求，；
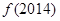（2）若，求证：；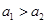
（3）求证：存在，使得．

凸边形中的每条边和每条对角线都被染为n种颜色中的一种颜色．问：对怎样的n，存在一种染色方式，使得对于这n种颜色中的任何3种不同颜色，都能找到一个三角形，其顶点为多边形的顶点，且它的3条边分别被染为这3种颜色？