高中数学合情推理和演绎推理填空题

观察下列等式
1＝1
2＋3＋4＝9
3＋4＋5＋6＋7＝25
4＋5＋6＋7＋8＋9＋10＝49
照此规律，第n个等式为__________________________________________________．

凸函数的性质定理为：如果函数在区间上是凸函数，则对于区间内的任意，有,已知函数在区间上是凸函数，则在中，的最大值为________．

在△ABC中，若D为BC 的中点，则有，将此结论类比到四面体中，在四面体 A-BCD中，若G为△BCD的重心，则可得一个类比结论：     ．

设函数f(x)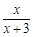＝(x＞0)，观察：f₁(x)＝f(x)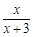＝, f₂(x)＝f(f₁(x))＝, f₃(x)＝f(f₂(x))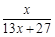＝, f₄(x)＝f(f₃(x))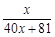＝……根据以上事实，由归纳推理可得：当n∈N*, n≥2时，f_n(x)＝f(_n－1(x))＝             ．

设的三边长分别为，的面积为，内切圆半径为，则；类比这个结论可知：四面体的四个面的面积分别为，内切球的半径为，四面体的体积为，则         .

对于实数，表示不超过的最大整数，观察下列等式：

按照此规律第个等式的等号右边的结果为               ．

已知点是函数的图象上任意不同两点，依据图象可知，线段AB总是位于A、B两点之间函数图象的上方，因此有结论成立．运用类比思想方法可知，若点是函数的图象上任意不同两点，则类似地有_________________成立．

古希腊毕达哥拉斯学派的数学家研究过各种多边形数。如三角形数1,3,6,10，第n个三角形数为． 记第n个k边形数为N（n，k）（，以下列出了部分k边形数中第n个数的表达式：
三角形数            
四边形数            
五边形数            
六边形数            
……
可以推测的表达式，由此计算的值为_____________．

如图是网络工作者经常用来解释网络运作的蛇形模型：数字1出现在第1行；数字2,3出现在第2行；数字6,5,4(从左至右)出现在第3行；数字7,8,9,10出现在第4行，依此类推，则(1)按网络运作顺序第n行第1个数字(如第2行第1个数字为2，第3行第1个数字为4，…)是________；(2)第63行从左至右的第4个数字应是________．

古希腊毕达哥拉斯学派的数学家研究过各种多边形数．如三角形数1,3,6,10，…，第个三角形数为．记第个边形数为，以下列出了部分边形数中第个数的表达式：
三角形数    
正方形数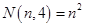     
五边形数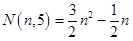     
六边形数     
……
可以推测的表达式，由此计算        ．

分形是几何学是美籍法国数学家伯努瓦·曼德尔布罗（BenoitMandelbrot）在20世纪70年代创立的一门新学科，它的创立为解决传统科学众多领域的难题提供了全新的思路．按照下图1的分形规律可得到如图2所示的一个树形图，则当时，第行空心圆点个数与第行及第行空心圆点个数的关系式为________；第12行的实心圆点的个数是_______．

如图.小正六边形沿着大正六边形的边按顺时针方向滚动，小正六边形的边长是大正六边形的边长的一半.如果小正六边形沿着大正六边形的边滚动一周后返回出发时的位置，在这个过程中，向量围绕着点旋转了角，其中为小正六边形的中心，则        .

对于实数，表示不超过的最大整数，观察下列等式：

按照此规律第个等式的等号右边的结果为               ．

记，当时，观察下列等式：
，，，，， ，可以推测           ．

当成等差数列时，有当成等差数列时，有当成等差数列时，有由此归纳，当 成等差数列时，有．如果成等比数列，类比上述方法归纳出的等式为______________．