高中数学合情推理和演绎推理填空题

设等差数列{a_n}的前n项和为S_n，则S₄，S₈－S₄，S₁₂－S₈，S₁₆－S₁₂成
等差数列．类比以上结论有：设等比数列{b_n}的前n项积为T_n，则T₄，________，________，成等比数列．

设函数f (x)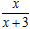＝ (x＞0)，观察：f ₁(x)＝f (x)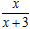＝， f ₂(x)＝f (f ₁(x))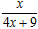＝，f ₃(x)＝f (f ₂(x))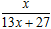＝，f ₄(x)＝f (f ₃(x))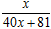＝……，根据以上事实，由归纳推理可得：当n∈N^*，n≥2时，f_n(x)＝f (f_n－1(x))＝           .

设函数f(x)＝ (x>0)，观察f₁(x)＝f(x)＝，
f₂(x)＝f[f₁(x)]＝，
f₃(x)＝f[f₂(x)]＝，
f₄(x)＝f[f₃(x)]＝，…
根据以上事实，由归纳推理可得：当n∈N_＋且n≥2时，f_n(x)＝f[f_n－1(x)]＝________.

设函数f(x)＝ (x>0)
观察：f₁(x)＝f(x)＝，f₂(x)＝f(f₁(x))＝，f₃(x)＝f(f₂(x))＝，
f₄(x)＝f(f₃(x))＝， 根据以上事实，由归纳推理可得：
当n∈N^*且n≥2时，f_n(x)＝f(f_n－1(x))＝________.

设P是边长为a的正△ABC内的一点,P点到三边的距离分别为h₁、h₂、h₃,则h₁+h₂+h₃=a;类比到空间,设P是棱长为a的空间正四面体ABCD内的一点,则P点到四个面的距离之和h₁+h₂+h₃+h₄=　　　　.

半径为r的圆的面积S(r)＝r²,周长C(r)=2r，若将r看作(0，＋∞)上的变量，则(r²)’＝2r ；对于半径为R的球，若将R看作(0，＋∞)上的变量，请你写出类似于上述的式子:_______________________.

定义映射f:A→B,其中A={(m,n)|m,n∈R},B=R,已知对所有的有序正整数对(m,n)满足下述条件:
①f(m,1)=1,②若n>m,f(m,n)=0;③f(m+1,n)=n[f(m,n)+f(m,n-1)],则f(2,2)=　　　　;f(n,2)=　　　　.

有一个数阵如下：记第行的第个数字为，（如），则等于        .

如图所示的三角形数阵叫“牛顿调和三角形”，它们是由整数的倒数组成的，第n行有n个数且两端的数均为，每个数是它下一行左右相邻两数的和，如 
，…，

则（1）第6行第2个数（从左往右数）为_________；
（2）第n行第3个数（从左往右数）为_________．

二维空间中圆的一维测度（周长），二维测度（面积），观察发现；三维空间中球的二维测度（表面积），三维测度（体积），观察发现．已知四维空间中“超球”的三维测度，猜想其四维测度______．

已知命题：在平面直角坐标系xOy中，椭圆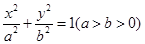，△ABC的顶点B在椭圆上，顶点A，C分别为椭圆的左、右焦点，椭圆的离心率为e，则，现将该命题类比到双曲线中，△ABC的顶点B在双曲线上，顶点A、C分别为双曲线的左、右焦点，设双曲线的方程为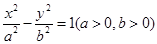．双曲线的离心率为e，则有________．

对于实数，表示不超过的最大整数，观察下列等式：

按照此规律第个等式的等号右边的结果为           ．

把正整数按一定的规则排成了如图所示的三角形数表．

设是位于这个三角形数表中从上往下数第行、从左往右数第个数，如．则             ．

依此类推，第个等式为                    ．

在平面几何中有如下结论：若正三角形ABC的内切圆面积为，外接圆面积为，则.推广到空间几何体中可以得到类似结论：若正四面体ABCD的内切球体积为，外接球体积为，则=___________.