高中数学空间向量的应用试题

在正方体ABCD-A₁B₁C₁D₁中，求证:AC₁BD.

设α，β，γ是三个互不重合的平面，m，n是两条不重合的直线，则下列命题中正确的是

A．若α⊥β，β⊥γ，则α⊥γ	B．若α//β，mβ，m//α，则m//β
C．若α⊥β，m⊥α，则m//β	D．若m//α，n//β，α⊥β，则m⊥n

在正方体中，若点（异于点）是棱上一点，则满足与所成的角为的点的个数为
                                                   

A．0

B．3

C．4

D．6

已知平面，直线，且，则“且”是“”的

A．充分不必要条件	B．必要不充分条件
C．充分必要条件	D．既不充分也不必要条件

（本小题满分14分）如图,在底面为平行四边形的四棱锥中,,平面,且,点是的中点.
求证:(1) 平面;        
(2)平面

（本小题满分14分）如图，在四棱锥中，底面为菱形，⊥平面，为的中点，为的中点，

求证：（Ⅰ）平面⊥平面；（Ⅱ）//平面.

如图，已知在侧棱垂直于底面三棱柱ABC—A₁B₁C₁中,AC=3，AB=5，BC=4,AA₁=4,点D是AB的中点.                
（Ⅰ）求证：AC⊥BC₁;
（Ⅱ）求证：AC₁∥平面CDB₁.

如图，ABCD－A₁B₁C₁D₁为正方体，下面结论中正确的是_____________.

①　AC∥平面CB₁D₁；
②　AC₁⊥平面CB₁D₁；
③　AC₁与底面ABCD所成角的正切值是；
④　与BD为异面直线。

如图，在直三棱柱中，，点是的中点.
求证：（1）；（2）平面.

已知为互不重合的平面，为互不重合的直线，给出下列四个命题：
①；
②；
③；
④.
其中正确命题的序号是____   ▲ __ __．

已知中，面，，求证：面．

如图所示，四边形ABCD中，AD//BC，AD=AB，∠BCD=45°，∠BAD=90°，将△ABD沿BD折起，使平面ABD⊥平面BCD，构成三棱锥A—BCD，则在三棱锥A—BCD中，下列命题正确的是（   ）

A．平面ABD⊥平面ABC	B．平面ADC⊥平面BDC
C．平面ABC⊥平面BDC	D．平面ADC⊥平面ABC

已知直线l、m 、n 与平面α、β给出下列四个命题：
①若m∥l，n∥l，则m∥n； ②若m⊥α，m∥β，则α⊥β；
③若m∥α，n∥α，则m∥n；④若m⊥β，α⊥β，则m∥α
其中，假命题的个数是（   ）

A．1

B．2

C．3

D．4

设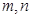是两条不同的直线，是两个不同的平面，有下列四个命题:
①若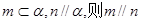  
②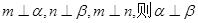
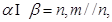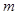③若则∥且∥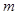
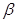
④若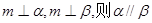
其中正确的命题是   ▲   ．（写出所有真命题的序号）．

设为两条不同的直线，为两个不同的平面，下列命题中正确的是           ．（填序号）
①若则；②若则；
③若则；④若则．