如图所示,AD⊥平面ABC,CE⊥平面ABC,AC=AD=AB=1, ,凸多面体ABCED的体积为
,凸多面体ABCED的体积为 ,F为BC的中点.
,F为BC的中点.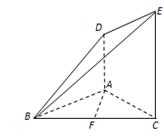
(1)求证:AF∥平面BDE;
(2)求证:平面BDE⊥平面BCE.
如图,已知六棱锥P﹣ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB则下列结论正确的是( )

| A.PB⊥AD |
| B.平面PAB⊥平面PBC |
| C.直线BC∥平面PAE |
| D.直线PD与平面ABC所成的角为45° |
已知某几何体的三视图和直观图如图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形.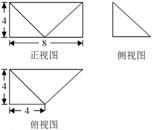

(Ⅰ)求证: ;
;
(Ⅱ)求直线 与平面
与平面 所成角的余弦值;
所成角的余弦值;
(Ⅲ)设 为
为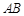 中点,在棱
中点,在棱 上是否存在一点
上是否存在一点 ,使
,使 平面
平面 ?若存在,求
?若存在,求 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
如图所示,在直三棱柱ABC-A1B1C1中, BC="AC" ,AC1⊥A1B,M,N分别是A1B1,AB的中点,给出下列结论:①C1M⊥平面A1ABB1,②A1B⊥NB1 ,③平面AMC1⊥平面CBA1 ,其中正确结论的个数为 ( )

| A.0 | B.1 | C.2 | D.3 |
已知 的三边长分别为
的三边长分别为 ,
, ,
, ,
, 是
是 边上的点,
边上的点, 是平面
是平面 外一点.给出下列四个命题:
外一点.给出下列四个命题:
①若 平面
平面 ,且
,且 是
是 边中点,则有
边中点,则有 ;
;
②若 ,
, 平面
平面 ,则
,则 面积的最小值为
面积的最小值为 ;
;
③若 ,
, 平面
平面 ,则三棱锥
,则三棱锥 的外接球体积为
的外接球体积为 ;
;
④若 ,
, 在平面
在平面 上的射影是
上的射影是 内切圆的圆心,则三棱锥
内切圆的圆心,则三棱锥 的体积为
的体积为 ;
;
其中正确命题的序号是 (把你认为正确命题的序号都填上).
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.
(1)证明:D1E⊥A1D;
(2)当E为AB的中点时,求点E到面ACD1的距离;
(3)AE等于何值时,二面角D1-EC-D的大小为 .
.
如图,三棱柱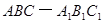 中,
中,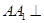 平面ABC,AB
平面ABC,AB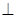 BC , 点M , N分别为A1C1与A1B的中点.
BC , 点M , N分别为A1C1与A1B的中点.
(Ⅰ)求证:MN 平面BCC1B1;
平面BCC1B1;
(Ⅱ)求证:平面A1BC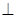 平面A1ABB1.
平面A1ABB1.
试题篮
()