如图,己知平行四边形ABCD中,∠ BAD = 600,AB=6, AD=3,G为CD中点,现将梯形ABCG沿着AG折起到AFEG。
(I)求证:直线CE//平面ABF;
(II)如果FG⊥平面ABCD求二面B一EF一A的平面角的余弦值.
(Ⅲ)若直线AF与平面 ABCD所成角为 ,求证:FG⊥平面ABCD
,求证:FG⊥平面ABCD
已知直三棱柱 中, 为 的中点.

(Ⅰ)求点 到平面 的距离;
(Ⅱ)若 ,求二面角 的平面角的余弦值.
在如图所示的几何体中,四边形 是等腰梯形, , 平面 .

(Ⅰ)求证:
平面
;
(Ⅱ)求二面角
的余弦值.
如图,在三棱锥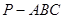 中,
中, ,
, 为
为 的中点,
的中点, 平面
平面 ,垂足
,垂足 落在线段
落在线段 上,已知
上,已知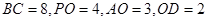 。
。
(Ⅰ)证明: ;
;
(Ⅱ)在线段 上是否存在点M,使得二面角
上是否存在点M,使得二面角 为直二面角?若存在,求
为直二面角?若存在,求
出AM的长;若不存在,请说明理由。
在四棱锥 中,底面
中,底面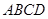 是矩形,已知
是矩形,已知 ,
,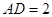 ,
, ,
,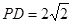 ,
, 。
。
(Ⅰ)求证: 平面
平面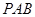 ;
;
(Ⅱ)求二面角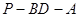 的正切值的大小。
的正切值的大小。
如图,在四棱锥 中,平面
中,平面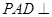 平面
平面 ,
, ,
,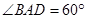 ,
,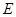 、
、 分别是
分别是 、
、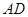 的中点。
的中点。
求证:(Ⅰ)直线 平面
平面 ;
;
(Ⅱ)平面 平面
平面 。
。
把长、宽各为4、3的长方形ABCD沿对角线AC折成直二面角,求顶点B和D的距离。
如图所示,在直三棱柱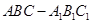 中,
中,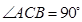 ,
,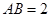 ,
,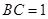 ,
,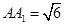 ,
,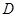 是棱
是棱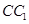 的中点.
的中点.
(1)证明: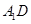
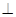 平面
平面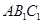 ;
;
(2)求二面角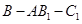 的余弦值.
的余弦值.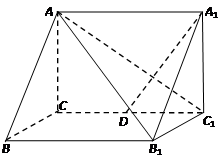
如图,四棱锥 的底面
的底面 是矩形,
是矩形,
 ,且侧面
,且侧面 是正三角形,平面
是正三角形,平面 平面
平面 ,
,
(Ⅰ)求证: ;
;
(Ⅱ)在棱 上是否存在一点
上是否存在一点 ,使得二面角
,使得二面角 的大小为45°.若存在,试求
的大小为45°.若存在,试求 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
试题篮
()