(本小题满分14分)已知四棱柱ABCD-A1B1C1D1的底面ABCD是边长为2的菱形, AC∩BD="O," AA1=2 , BD⊥A1A, ∠BAD=∠A1AC="60°," 点M是棱AA1的中点.
, BD⊥A1A, ∠BAD=∠A1AC="60°," 点M是棱AA1的中点.
(1)求证: A1C∥平面BMD;
(2)求证: A1O⊥平面ABCD;
(3)求直线BM与平面BC1D所成角的正弦值.
如图,等腰梯形ABEF中,AB//EF,AB=2,AD=AF=1,AF⊥BF,O为AB的中点,矩形ABCD所在平面与平面ABEF互相垂直.
(1)求证:AF⊥平面CBF;
(2)在棱FC上是否存在点M,使得OM//平面DAF?
(3)求点A到平面BDF的距离.
(本小题满分13分)三棱锥P-DEF中, 顶点P在平面DEF上的射影为O.
(Ⅰ)如果PE=PF=PD, 证明O是三角形DEF的外心(外接圆的圆心)
(Ⅱ)如果 ,
,  ,
,  ,
,  ,证明: O是三角形DEF的垂心(三条高的交点)
,证明: O是三角形DEF的垂心(三条高的交点)
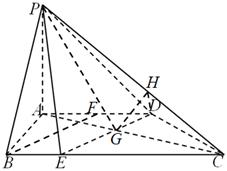
如图,在四棱锥 中,
中, //
// ,
, ,
, ,
, ,平面
,平面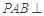 平面
平面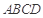 .
.
(1)求证:平面 平面
平面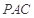 ;
;
(2)若直线 与平面
与平面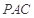 所成的角的正弦值为
所成的角的正弦值为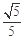 ,求二面角
,求二面角 的平面角的余弦值.
的平面角的余弦值.
(本小题满分14分)如图,在梯形 中,
中, ,
, ,四边形
,四边形 为矩形,平面
为矩形,平面 平面
平面 ,
, .
.
(1)求证: 平面
平面 ;
;
(2)点 在线段
在线段 上运动,设平面
上运动,设平面 与平面
与平面 所成二面角的平面角为
所成二面角的平面角为 ,试求
,试求 的取值范围.
的取值范围.
(本小题满分12分) 如图,在多面体ABCDEF中, ABCD为菱形, ,EC
,EC 面ABCD, FA
面ABCD, FA 面ABCD,G为BF的中点,若EG//面ABCD.
面ABCD,G为BF的中点,若EG//面ABCD.
(Ⅰ)求证:EG 面ABF;
面ABF;
(Ⅱ)若 ,求二面角B-EF-D 的余弦值.
,求二面角B-EF-D 的余弦值.
如图1, 是直角△
是直角△ 斜边上的高,沿
斜边上的高,沿 把△
把△ 的两部分折成直二面角(如图2),
的两部分折成直二面角(如图2), 于
于 .
.
(Ⅰ)证明: ;
;
(Ⅱ)设 ,
, 与平面
与平面 所成的角为
所成的角为 ,二面角
,二面角 的大小为
的大小为 ,试用
,试用 表示
表示 ;
;
(Ⅲ)设 ,
, 为
为 的中点,在线段
的中点,在线段 上是否存在一点
上是否存在一点 ,使得
,使得 ∥平面
∥平面 ? 若存在,求
? 若存在,求 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
试题篮
()