已知直线 ,
, 和平面
和平面 且
且 ,给出下列四个命题:
,给出下列四个命题:
① ②
② ③
③ ④
④
其中真命题的有________(请填写全部正确命题的序号)
下面是空间线面位置关系中传递性的部分相关命题:
①与两条平行线中一条平行的平面必与另一条直线平行;
②与两条平行线中一条垂直的平面 必与另一条直线垂直;
③与两条垂直直线中一条平行的平面必与另一条直线垂直;
④与两条垂直直线中一条垂直的平面必与另一条直线平行;
⑤与两个平行平面中一个平行的直线必与另一个平面平行;
⑥与两个平行平面中一个垂直的直线必与另一个平面垂直;
⑦与两个垂直平面中一个平行的直线必与另一个平面垂直;
⑧与两个垂直平面中一个垂直的直线必与另一个平面平行.
其中正确的命题个数有________个.
下列命题中:
(1)、平行于同一直线的两个平面平行;
(2)、平行于同一平面的两个平面平行;
(3)、垂直于同一直线的两直线平行;
(4)、垂直于同一平面的两直线平行.
其中所有正确的命题有_____________。
已知直线 ,平面
,平面 ,且
,且 ,
, ,给出下列四个命题:
,给出下列四个命题:
①若 ∥
∥ ,则
,则 ;②若
;②若 ,则
,则 ∥
∥ ;
;
③若 ,则
,则 ∥
∥ ;④若
;④若 ∥
∥ ,则
,则 ;
;
其中为真命题的序号是_______
已知平面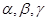 ,直线
,直线 满足:
满足: ,那么
,那么
①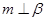 ; ②
; ②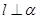 ; ③
; ③ ; ④
; ④ 。
。
可由上述条件可推出的结论有 ;
给出下列四个命题:
①过平面外一点,作与该平面成 角的直线一定有无穷多条。
角的直线一定有无穷多条。
②一条直线与两个相交平面都平行,则它必与这两个平面的交线平行;
③对确定的两条异面直线,过空间任意一点有且只有一个平面与这两条异面直线都平行;
④对两条异面的直线,都存在无穷多个平面与这两条直线所成的角相等;
其中正确的命题序号为
已知 是两个不同的平面,m、n是平面
是两个不同的平面,m、n是平面 之外的两条不同的直线,给出四个论断: ①m⊥n,②
之外的两条不同的直线,给出四个论断: ①m⊥n,② ,③
,③ ,④
,④ 。
。
以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个命题________。
如图甲,在△ABC中,AB⊥AC,AD⊥BC,
D是垂足,则AB2=BD·BC,该结论称为射
影定理。如图乙,在三棱锥A—BCD中,
AD⊥平面ABC,AO⊥平面BCD,O为垂
足,且O在△BCD内,类比射影定理,探
究S△BCO、S△BCD、S△ABC这三者之间满足的
关系式是 。
试题篮
()