高中数学平行线法试题

（本小题满分12分）如图，直三棱柱ABC-A₁B₁C₁，∠ACB=90°，E是棱C₁的中点，且CF⊥AB，AC=BC．

（1）求证：CF∥平面AEB1；
（2）求证：平面AEB₁⊥平面ABB₁A₁．

如图所示，已知空间四边形的每条边和对角线长都等于1，点，，分别是、、的中点，计算：

（1）；
（2）的长；
（3）异面直线与所成角的余弦值．

（本小题满分12分）已知直四棱柱的底面是菱形，且，为棱的中点为线段的中点．

（1）求证：直线；
（2）求证：

下图是一个正三棱柱（以为底面）被一平面所截得到的几何体，截面为．已知，，，．

（1）设点是的中点，证明：平面；
（2）求与平面所成的角的正弦值；

如图，四棱锥中，四边形是正方形，若分别是线段的中点．

（1）求证：||底面；
（2）若点为线段的中点，平面与平面有怎样的位置关系？并证明。

，是直线上的两点，，于，于，，且直线与直线成的角，则、两点间的距离是_______．

设a，b，c是空间三条直线，，是空间两个平面，则下列命题中，逆命题不成立的是（   ）

A．当c⊥时，若c⊥，则∥

B．当时，若b⊥，则

C．当，且c是a在内的射影时，若b⊥c，则a⊥b

D．当，且时，若c∥，则b∥c

在四棱锥中，平面，底面为直角梯形，，，且为的中点．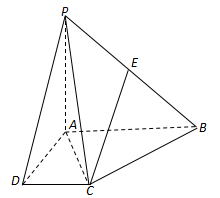

（1）求证：平面；
（2）求直线与平面所成角的正切值．

如图，直三棱柱ABC﹣A₁B₁C₁中，AC⊥BC，AC=BC=CC₁=2，M，N分别为AC，B₁C₁的中点．

（Ⅰ）求证：MN∥平面ABB₁A₁；
（Ⅱ）线段CC₁上是否存在点Q，使A₁B⊥平面MNQ？说明理由．

在正三棱锥中，、分别为棱、的中点，且。

（1）求证：直线平面；
（2）求证：平面平面。

如图，在四棱锥P-ABCD 中，AB∥CD ，AB⊥AD，CD=2AB，平面PAD⊥底面ABCD，PA⊥AD，E和F分别为CD和PC的中点．求证：

（1）BE∥平面PAD；
（2）平面BEF⊥平面PCD．

若P两条异面直线l，m外的任意一点，则（ ）

A．过点P有且仅有一条直线与l，m都平行

B．过点P有且仅有一条直线与l，m都垂直

C．过点P有且仅有一条直线与l，m都相交

D．过点P有且仅有一条直线与l，m都异面

如图所示，在直三棱柱ABC﹣A₁B₁C₁中，AB=BC=BB₁，D为AC的中点．

（I）求证：B₁C∥平面A₁BD；
（Ⅱ）若AC₁⊥平面A₁BD，求证：B₁C₁⊥平面ABB₁A₁；
（Ⅲ）在（II）的条件下，求二面角B﹣A₁C₁﹣D的大小．

如图，已知四棱锥的底面是正方形，侧棱底面．

（1）若，是的中点．证明：平面；
（2）若二面角的余弦值为，试求的值．

如图，在正方体ABCD-A₁B₁C₁D₁中．
 
（1）若E为棱DD₁上的点，试确定点E的位置，使平面A₁C₁E∥B₁D； 
（2）若M为A₁B上的一动点，求证：DM∥平面D₁B₁C．