高中数学平面解析几何的产生──数与形的结合试题

椭圆与双曲线有相同的焦点，则a的值是（ ）

A．

B．1或–2

C． 1或

D． 1

已知直线经过点。
（I）求的值；
（II）若直线过点且，求直线的方程。

已知，则的最大值为          

已知直线与直线平行,求a的值.

已知，，则线段的中点的坐标是________.

圆 内有一点，AB为过点且倾斜角为α的弦，
（1） 当时，求AB的长;
（2）当弦AB被点平分时，写出直线AB 的方程。

已知椭圆E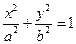：（0）过点（0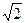，），其左焦点与点P（1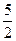，）的连线与圆相切。
（1）求椭圆E的方程；
（2）设Q为椭圆E上的一个动点，试判断以为直径的圆与圆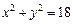的位置关系，并证明

求过点2x+y+8=0和x+y+3=0的交点，且与直线2x+3y-7=0垂直的直线方程。        

（本小题满分10分）选修4-4：坐标系与参数方程
在极坐标系中，已知圆的圆心坐标为，半径为，点在圆周上运动，
（Ⅰ）求圆的极坐标方程；
（Ⅱ）设直角坐标系的原点与极点重合，轴非负半轴与极轴重合，为中点，求点的参数方程.

(本题满分15分)圆C过点A（2,0）及点B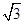（，），且与直线l:y=相切
（1）求圆C的方程；
（2）过点P（2,1）作圆C的切线,切点为M,N，求|MN|；
（3）点Q为圆C上第二象限内一点，且∠BOQ=，求Q点横坐标.

已知平面上的线段及点，在上任取一点，线段长度的最小值称为点到线段的距离，记作．设是长为2的线段，点集所表示图形的面积为      

已知命题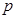: 双曲线的离心率小于1. 则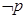为

A．双曲线的离心率大于1	B．有的双曲线离心率小于1
C．有的双曲线离心率大于1	D．存在双曲线, 其离心率不小于1

将直线绕点（1，0）沿逆时针方向旋转得到直线，则直线与圆的位置关系是

A．相交

B．相切

C．相离

D．相交或相切

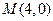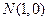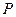（本小题满分12分）已知，，若动点满足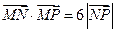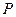，点的轨迹为曲线.
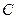（Ⅰ）求曲线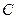的方程；
（Ⅱ）试确定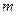的取值范围，使得对于直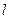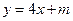线：，曲线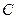上总有不同的两点关于直线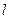对称.

设圆锥曲线 C的两个焦点分别为F₁、F₂，若曲线C上存在点P满足|PF₁|:|F₁F₂|:|PF₂|=4:3:2，则圆锥曲线C的离心率等于

A．或

B．或2

C．或2

D．或