( 10分)已知双曲线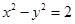 的左、右焦点分别为
的左、右焦点分别为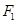 ,
, ,过点
,过点 的动直线与双曲线相交于
的动直线与双曲线相交于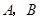 两点.
两点.
(I)若动点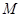 满足
满足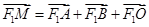 (其中
(其中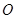 为坐标原点),求点
为坐标原点),求点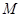 的轨迹方程;
的轨迹方程;
(II)在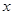 轴上是否存在定点
轴上是否存在定点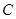 ,使
,使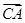 ·
·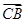 为常数?若存在,求出点
为常数?若存在,求出点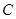 的坐标;
的坐标;
若不存在,请说明理由.
已知圆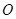 的半径为定长
的半径为定长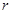 ,
,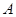 是圆所在平面内一定点,
是圆所在平面内一定点,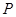 是圆上任意一点,线段
是圆上任意一点,线段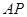 的垂直平分线
的垂直平分线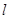 与直线
与直线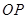 相交于点
相交于点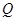 ,当
,当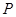 在圆上运动时,点
在圆上运动时,点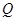 的轨迹可能是下列图形中的: .(填写所有可能图形的序号)
的轨迹可能是下列图形中的: .(填写所有可能图形的序号)
①点;②直线;③圆;④抛物线;⑤椭圆;⑥双曲线;⑦双曲线的一支.
已知点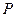 为圆周
为圆周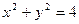 的动点,过
的动点,过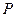 点作
点作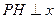 轴,垂足为
轴,垂足为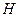 ,设线段
,设线段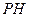 的中点为
的中点为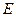 ,记点
,记点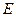 的轨迹方程为
的轨迹方程为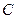 ,点
,点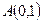
(1)求动点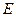 的轨迹方程
的轨迹方程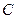 ;
;
(2)若斜率为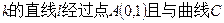 的另一个交点为
的另一个交点为 ,求
,求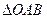 面积的最大值及此时直线
面积的最大值及此时直线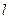 的方程;
的方程;
(3)是否存在方向向量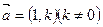 的直线
的直线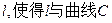 交与两个不同的点
交与两个不同的点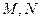 ,且有
,且有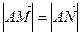 ?若存在,求出
?若存在,求出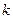 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。
互相平行的三条直线,最多可以确定的平面个数为( )
| A.1个 | B.2个 | C.3个 | D.4个 |
已知椭圆E: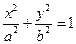 (
(


 0)过点(0,
0)过点(0,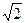 ),其左焦点
),其左焦点 与点P(1,
与点P(1,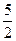 )的连线与圆
)的连线与圆 相切。
相切。
(1)求椭圆E的方程;
(2)设Q为椭圆E上的一个动点,试判断以 为直径的圆与圆
为直径的圆与圆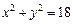 的位置关系,并证明
的位置关系,并证明
(本小题满分10分)选修4-4:坐标系与参数方程
在极坐标系中,已知圆 的圆心坐标为
的圆心坐标为 ,半径为
,半径为 ,点
,点 在圆周上运动,
在圆周上运动,
(Ⅰ)求圆 的极坐标方程;
的极坐标方程;
(Ⅱ)设直角坐标系的原点与极点 重合,
重合, 轴非负半轴与极轴重合,
轴非负半轴与极轴重合, 为
为 中点,求点
中点,求点 的参数方程.
的参数方程.
已知命题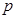 : 双曲线的离心率小于1. 则
: 双曲线的离心率小于1. 则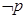 为
为
| A.双曲线的离心率大于1 | B.有的双曲线离心率小于1 |
| C.有的双曲线离心率大于1 | D.存在双曲线, 其离心率不小于1 |
(本小题满分12分)已知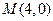 ,
,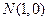 ,若动点
,若动点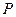 满足
满足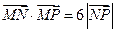 ,
,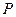 点的轨迹为曲线
点的轨迹为曲线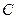 .
.
(Ⅰ)求曲线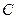 的方程;
的方程;
(Ⅱ)试确定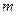 的取值范围,使得对于直线
的取值范围,使得对于直线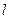 :
: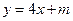 ,曲线
,曲线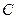 上总有不同的两点关于直线
上总有不同的两点关于直线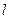 对称.
对称.
试题篮
()