给出如下两个命题:命题A:函数 为增函数;命题B:方程
为增函数;命题B:方程 (
( )有虚根.若A与B中有且仅有一个是真命题,则实数
)有虚根.若A与B中有且仅有一个是真命题,则实数 的取值范围是___________________
的取值范围是___________________
(本小题满分14分) 对于函数f(x), 若存在x0∈R,使f(x0)=x0成立, 则称x0为f(x)的不动点. 已知函数f(x)=ax2+(b+1)x+b-1(a≠0)
若存在x0∈R,使f(x0)=x0成立, 则称x0为f(x)的不动点. 已知函数f(x)=ax2+(b+1)x+b-1(a≠0)
(1)当a=1,b=-2时,求f(x)的不动点;
(2)若对于任意实数b,函数f(x)恒有两个相异的不动点,求a的取值范围
若不等式(a-2)x2+2(a-2)x-4<0对一切x∈R恒成立,则a的取值范围是 ( )
A.(-2,2 |
B.(-∞,2 |
C. -2,2 -2,2 |
D.(-∞,-2) |
函数 的图像可以看作由函数
的图像可以看作由函数 的图象,经过下列的平移得到 ( )
的图象,经过下列的平移得到 ( )
| A.向右平移6,再向下平移8 | B.向左平移6,再向下平移8 |
| C.向右平移6,再向上平移8 | D.向左平移6,再向上平移8 |
已知函数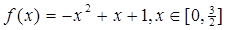 的最值情况为( )
的最值情况为( )
A.有最小值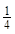 ,有最大值1 ,有最大值1 |
B.有最小值 ,有最大值 ,有最大值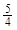 |
C.有最小值1,有最大值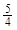 |
D.有最小值,无最大值 |
已知函数f(x)=x2+2x+alnx,若函数f(x)在(0,1)上单调,则实数a的取值范围是( )
| A.a≥0 | B.a<-4 | C.a≥0或a≤-4 | D.a>0或a<-4 |
试题篮
()