高中数学二次剩余选择题

二次函数f(x)=ax2+bx+c的图象的开口向下,对称轴为x=1,方程 ax2+bx+c=0的两个解一个在区间(2,3)中,则下列判断正确的是

A．abc>0

B．a+b+c<0

C．a-b+c<0

D．3b<2c

已知函数的图像与函数的图像关于直线对称，那么下列情形不可能出现的是（  ）

A．函数有最小值	B．函数过点（4，2）
C．函数是偶函数	D．函数在其定义域上是增函数

已知过点（1，2）的二次函数的图象如右图，
给出下列论断：①，②,③，④. 其中正确论断是

A．①③

B．②④

C．②③

D．②③④

已知函数，且的解集为（－2，1）则函数的图象为（ ）

 

 

已知函数满足,且,当时(   )

A．

B．

C．

D．以上皆不对.

设 若对于任意总存在
使得成立，则的取值范围是（   ）

A．

B．

C．

D．

已知函数f(x)=ax²-(3-a)x+1，g(x)=x，若对于任一实数x，f(x)与g(x)至少有一个为正数，
则实数a的取值范围是

A．［0,3)

B．［3,9)

C．［1,9)

D．［0,9)

若与在区间上都是减函数，则a的取值范围是（）
A．              B．              C．           D．
8．求下列函数的零点，可以采用二分法的是（ B ）
A．                                                 B．
C．                                      D．

点在函数的图象上，点与点关于轴对称,且在直线上，则函数在区间上           （   ）

A．既没有最大值也没有最小值	B．最小值为-3，无最大值
C．最小值为-3，最大值为9	D．最小值为，无最大值

函数y="2x" -的图像大致是 （     ）                                          

函数在区间上有最小值，则函数在区间上一定（  ）

A．有最小值

B．有最大值

C．是减函数

D．是增函数

函数y＝x2－2x在区间[a，b]上的值域是[－1，3]，

则点(a，b)的轨迹是图中的

A．线段AB和线段AD	B．线段AB和线段CD
C．线段AD和线段BC	D．线段AC和线段BD

若二次函数在区间上为减函数，那么（  ）

A．

B．

C．

D．

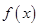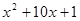已知函数=，则函数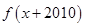的最小值及对称轴方程分别为（    ）

A．-24，-2015

B．24，x=“-2015”

C．24，x=“2015”

D．-24，x=-2015

已知实系数方程的两个实数根分别是，且，则的取值范围是  (     ) 

A．

B．

C．

D．