高中数学二次剩余解答题

已知函数
（1）若的解集为，求实数的取值范围;
（2）在(1)的条件下,求函数f(x)在区间[0,3]的值域.

已知是二次函数，且
（1）求的解析式；
（2）求函数的单调递减区间及值域。

（１）解关于的不等式；
（２）若关于的不等式有解，求实数的取值范围．

设，若，，．
（1）若，求的取值范围；
（2）判断方程在内实根的个数．

已知二次函数的二次项系数为，且不等式的解集为,
（1）若方程有两个相等的根，求的解析式；
（2）若的最大值为正数，求的取值范围．

函数在闭区间上的最小值记为
（1）求的函数表达式；
（2）作的图像，并写出的最小值．

已知a、b、c是互不相等的非零实数.若用反证法证明三个方程ax²+2bx+c=0，bx²+2cx+a=0，cx²+2ax+b=0至少有一个方程有两个相异实根.

已知二次函数的二次项系数为，满足不等式的解集为（1，3），且方程有两个相等的实根，求的解析式.

已知二次函数.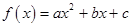
（1）若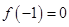，试判断函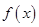数零点个数
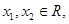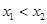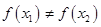（2）若对且，，证明方程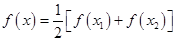必有一个实数根属于。
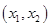（3）是否存在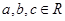，使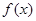同时满足以下条件①当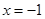时， 函数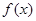有最小值0；；②对任意实数x,都有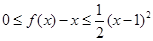。若存在，求出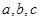的值，若不存在，请说明理由。

已知函数f（x）=x²+2x+alnx（a∈R）．
（1）当时a=﹣4时，求f（x）的最小值；
（2）若函数f（x）在区间（0，1）上为单调函数，求实数a的取值范围．

已知函数，
（1）求在区间的最小值；（2）求在区间的值域

已知二次函数满足．
（1）求的解析式；
（2）若在上有最小值，最大值，求a的取值集合．

（本小题满分14分）函数和的图象的示意图如图所示，设两函数的图象交于点 ，，且．

（1）请指出示意图中曲线，分别对应哪一个函数?
（2）证明：，且；
（3）结合函数图象的示意图，判断，，，的大小，并按从小到大的顺序排列．

已知函数.
(1)若的定义域和值域均是，求实数的值；
(2)若在区间上是减函数，且对任意的，，总有，求实数的取值范围.

求函数f(x)="sinx+cosx+sinxcosx." x∈﹝0,﹞的最大值并求出相应的x值.