高中数学二次剩余解答题

（本小题共14分）函数，，.
（1）①试用含有的式子表示；②求的单调区间；
（2）对于函数图像上的不同两点，，如果在函数图像上存在点（其中在与之间），使得点处的切线∥，则称存在“伴随切线”，当时，又称存在“中值伴随切线”。试问：在函数的图像上是否存在两点、，使得存在“中值伴随切线”？若存在，求出、的坐标；若不存在，说明理由。

已知函数（）．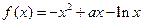
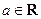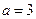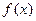（1）当时，求函数在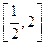上的最大值和最小值；
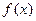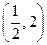（2）当函数在单调时，求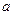的取值范围；
（3）求函数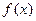既有极大值又有极小值的充要条件。

（（本小题满分14分）设函数，。
⑴ 若，过两点和的中点作轴的垂线交曲线 于点，求证：曲线在点处的切线过点；
⑵ 若，当时恒成立，求实数的取值范围。

（本小题满分12分）
设函数.
（1）当时，求函数在区间上的最小值；
（2）当时，曲线在点处的切线为，与轴交于点
求证：.

（本小题满分12分）
已知二次函数的图象过点（0，-3），且的解集．
（Ⅰ）求的解析式；
（Ⅱ）求函数的最值．

（本小题满分15分）
设函数是定义在上的奇函数，当时，（a为实数）．
（1）当时，求的解析式；
（2）当时，试判断在上的单调性，并证明你的结论．

已知函数．
（Ⅰ）试求的值域；
(Ⅱ)设若对， ，恒成立，试求实数的取值范围

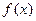二次函数满足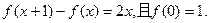
（1）求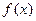的解析式；
（2）在区间[－1，1]上，y=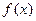的图象恒在的图象上方，试确定实数m的范围。

已知二次函数 
（Ⅰ）若的解集为求实数的值；
（Ⅱ）若满足且关于的方程的两个实数根分别在区间（-3，-2），（0，1）内，求实数的取值范围.

已知函数,若对于任意都成立，
求函数的值域．

(10分) 设函数求证：
（1）；
（2）函数在区间（0，2）内至少有一个零点；

（本小题满分14分）已知函数=
(1) 若存在单调增区间，求的取值范围；
（2）是否存在实数>0，使得方程在区间内有且只有两个不相等的实数根？若存在，求出的取值范围？若不存在，请说明理由．

已知函数(其中常数a,b∈R),是奇函数.
（1）求的表达式;（2）讨论的单调性，并求在区间[1,2]上的最大值和最小值.

已知二次函数的图像过点，又 
⑴求的解析式；   ⑵若有两个不等实根，求实数的取值范围。

（满分12分）
已知函数f ( x )=x ²+ax+b
（1）若f (x)在[ 1，+∞)内递增，求实数a的范围。
（2）若对任意的实数x都有f (1+x)="f" (1－x) 成立，
①求实数 a的值；
②证明函数f(x)在区间[1，＋∞上是增函数.