下列推理中属于归纳推理且结论正确的是( )
| A.由an=2n﹣1,求出S1=12,S2=22,S3=32,…,推断:数列{an}的前n项和Sn=n2 |
B.由f(x)=xcosx满足f(﹣x)=﹣f(x)对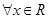 都成立,推断:f(x)=xcosx为奇函数 都成立,推断:f(x)=xcosx为奇函数 |
C.由圆x2+y2=r2的面积S=πr2,推断:椭圆 =1的面积S=πab =1的面积S=πab |
D.由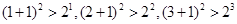 ,…,推断:对一切 ,…,推断:对一切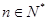 ,(n+1)2>2n ,(n+1)2>2n |
设函数 对任意实数x 、y都有
对任意实数x 、y都有 ,
,
(1)求 的值;
的值;
(2)若 ,求
,求 、
、 、
、 的值;
的值;
(3)在(2)的条件下,猜想
 的表达式,并用数学归纳法加以证明。
的表达式,并用数学归纳法加以证明。
用数学归纳法证明不等式“2n>n2+1对于n≥n0的自然数n都成立”时,第一步证明中的起始值n0应取为________.
在用数学归纳法证明 时,在验证当
时,在验证当 时,等式左边为( )
时,等式左边为( )
| A.1 | B. |
C. |
D. |
试题篮
()