设数列{an}满足a1=3,an+1=an2-2nan+2,n=1,2,3,…
(1)求a2,a3,a4的值,并猜想数列{an}的通项公式(不需证明);
(2)记Sn为数列{an}的前n项和,试求使得Sn<2n成立的最小正整数n,并给出证明.
已知f(n)=1+ +
+ +…+
+…+ (n∈N*),用数学归纳法证明f(2n)>
(n∈N*),用数学归纳法证明f(2n)> 时,f(2k+1)-f(2k)等于________.
时,f(2k+1)-f(2k)等于________.
用数学归纳法证明“n3+(n+1)3+(n+2)3(n∈N*)能被9整除”,要利用归纳假设证n=k+1时的情况,只需展开( )
| A.(k+3)3 | B.(k+2)3 |
| C.(k+1)3 | D.(k+1)3+(k+2)3 |
设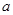 是一个自然数,
是一个自然数, 是
是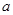 的各位数字的平方和,定义数列
的各位数字的平方和,定义数列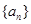 :
: 是自然数,
是自然数,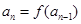 (
( ,
, ).
).
(1)求 ,
,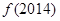 ;
;
(2)若 ,求证:
,求证: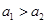 ;
;
(3)求证:存在 ,使得
,使得 .
.
设 是一个自然数,
是一个自然数, 是
是 的各位数字的平方和,定义数列
的各位数字的平方和,定义数列 :
: 是自然数,
是自然数, (
( ,
, ).
).
(1)求 ,
, ;
;
(2)若 ,求证:
,求证: ;
;
(3)当 时,求证:存在
时,求证:存在 ,使得
,使得 .
.
已知 ,
, ,
, .
.
(1)当 时,试比较
时,试比较 与
与 的大小关系;
的大小关系;
(2)猜想 与
与 的大小关系,并给出证明.
的大小关系,并给出证明.
在数列 中,已知
中,已知 ,
, ,
, (
( ,
, ).
).
(1)当 ,
, 时,分别求
时,分别求 的值,判断
的值,判断 是否为定值,并给出证明;
是否为定值,并给出证明;
(2)求出所有的正整数 ,使得
,使得 为完全平方数.
为完全平方数.
下面四个判断中,正确的是( )
| A.式子1+k+k2+…+kn(n∈N*)中,当n=1时式子值为1 |
| B.式子1+k+k2+…+kn-1(n∈N*)中,当n=1时式子值为1+k |
C.式子1+ +…+ +…+ (n∈N*)中,当n=1时式子值为1+ (n∈N*)中,当n=1时式子值为1+ |
D.设f(x)= (n∈N*),则f(k+1)=f(k)+ (n∈N*),则f(k+1)=f(k)+ |
(本小题满分13分)已知数列 中,
中,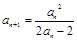 ,
,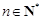 .
.
(Ⅰ)若 ,设
,设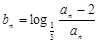 ,求证数列
,求证数列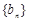 是等比数列,并求出数列
是等比数列,并求出数列 的通项公式;
的通项公式;
(Ⅱ)若 ,
, ,
,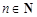 ,证明:
,证明: .
.
设数列{an}:1,-2,-2,3,3,3,-4,-4,-4,-4,…,(-1)k-1k,…,(-1) ,即当
,即当 (k∈N*)时,an=(-1)k-1k,记Sn=a1+a2+…+an(n∈N*),用数学归纳法证明Si(2i+1)=-i(2i+1)(i∈N*).
(k∈N*)时,an=(-1)k-1k,记Sn=a1+a2+…+an(n∈N*),用数学归纳法证明Si(2i+1)=-i(2i+1)(i∈N*).
试题篮
()