设 是一个自然数,
是一个自然数, 是
是 的各位数字的平方和,定义数列
的各位数字的平方和,定义数列 :
: 是自然数,
是自然数, (
( ,
, ).
).
(1)求 ,
, ;
;
(2)若 ,求证:
,求证: ;
;
(3)当 时,求证:存在
时,求证:存在 ,使得
,使得 .
.
已知 ,
, ,
, .
.
(1)当 时,试比较
时,试比较 与
与 的大小关系;
的大小关系;
(2)猜想 与
与 的大小关系,并给出证明.
的大小关系,并给出证明.
在数列 中,已知
中,已知 ,
, ,
, (
( ,
, ).
).
(1)当 ,
, 时,分别求
时,分别求 的值,判断
的值,判断 是否为定值,并给出证明;
是否为定值,并给出证明;
(2)求出所有的正整数 ,使得
,使得 为完全平方数.
为完全平方数.
(本小题满分12 分)已知函数 是定义在R上的不恒为零的函数,且对于任意的
是定义在R上的不恒为零的函数,且对于任意的 、
、 ∈R,都满足
∈R,都满足 ,若
,若 =1,
=1, .
.
(1)求 、
、 、
、 的值;
的值;
(2)猜测数列 通项公式,并用数学归纳法证明.
通项公式,并用数学归纳法证明.
(本小题满分13分)已知数列 中,
中,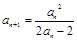 ,
,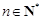 .
.
(Ⅰ)若 ,设
,设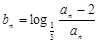 ,求证数列
,求证数列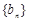 是等比数列,并求出数列
是等比数列,并求出数列 的通项公式;
的通项公式;
(Ⅱ)若 ,
, ,
,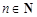 ,证明:
,证明: .
.
观察下列等式 第一个式子
第一个式子 第二个式子
第二个式子 第三个式子
第三个式子 第四个式子
第四个式子
照此规律下去
(Ⅰ)写出第 个等式;
个等式;
(Ⅱ)你能做出什么一般性的猜想?请用数学归纳法证明猜想.
【原创】
(1)观察下列各式;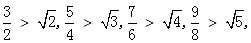 根据以上各式利用归纳推理得出一个一般性的结论;
根据以上各式利用归纳推理得出一个一般性的结论;
(2)设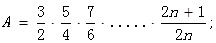
 根据
根据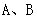 的大小关系证明(1)的结论;
的大小关系证明(1)的结论;
试题篮
()