高中数学第二数学归纳法试题

设，，， ，，
则 ___   ___．

平面内有n(n∈N_＋，n≥2)条直线，其中任何两条不平行，任何三条不过
同一点，证明：交点的个数f(n)＝.

用数学归纳法证明1²+3²+5²+…+（2n﹣1）²=n（4n²﹣1）过程中，由n=k递推到n=k+1时，不等式左边增加的项为（　　）

A．（2k）^2

B．（2k+3）^2

C．（2k+2）^2

D．（2k+1）^2

用数学归纳法证明不等式:++…+>(n∈N^*且n>1).

已知函数，数列满足，．
（1）求；
（2）猜想数列的通项，并用数学归纳法予以证明．

已知函数
（Ⅰ）若函数在其定义域上为单调函数,求的取值范围；
（Ⅱ）若函数的图像在处的切线的斜率为0，，已知求证：
（Ⅲ）在（2）的条件下，试比较与的大小，并说明理由.      

在数列中，，且. 求，猜想的表达式，并加以证明.

已知函数，当时，函数取得极大值.
（１）求实数的值；
（２）已知结论：若函数在区间内导数都存在，且，则存在，使得.试用这个结论证明：若，函数，则对任意，都有；
（３）已知正数，满足，求证：当，时，对任意大于，且互不相等的实数，都有.

已知为等差数列，且，公差.
（1）数列满足结论；；试证：；
（2）根据（1）中的几个等式，试归纳出更一般的结论，并用数学归纳法证明.

已知数列的前n项和为，且，令.
（1）求证：数列是等差数列，并求数列的通项公式；
（2）若，用数学归纳法证明是18的倍数．

设函数其中是的导函数．
（1）令，猜测的表达式并给予证明；
（2）若恒成立，求实数的取值范围；
（3）设，比较与的大小，并说明理由．

利用数学归纳法证明“”，在验证成立时，等号左边是     （     ）

A．

B．

C．

D．

在数列中，已知，且。
（1）用数学归纳法证明：；
（2）求证．

【原创】
（1）观察下列各式;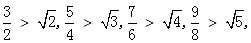根据以上各式利用归纳推理得出一个一般性的结论；
（2）设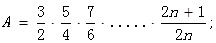根据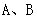的大小关系证明（1）的结论；

设实数 $c>0$，整数 $p>1,n\in N^{+}$.
（1）证明：当 $x>-1$且 $x\ne 0$时， $(1+x{)}^p>1+px$；
（2）数列 $\left\{a_n\right\}$满足 $a_1>c^{\frac{1}{p}},a_{n+1}=\frac{p-1}{p}{a}_n+\frac{c}{p}{a_n}^{1-p}$，证明： $a_n>a_{n+1}>c^{\frac{1}{p}}$.