某商品在近30天内每件的销售价格p(元)与时间t(天)的函数关系是 该商品的日销售量Q(件)与时间t(天)的函数关系是
该商品的日销售量Q(件)与时间t(天)的函数关系是
 ,求这种商品的日销售金额的最大值,并指出日销售金额最大的一天是30天中的第几天?
,求这种商品的日销售金额的最大值,并指出日销售金额最大的一天是30天中的第几天?
对于二次函数 ,
,
(1)指出图像的开口方向、对称轴方程、顶点坐标;
(2)画出它的图像,并说明其图像由 的图像经过怎样平移得来;
的图像经过怎样平移得来;
(3)求函数的最大值或最小值;
(4)分析函数的单调性。
在平面直角坐标系 中,函数
中,函数 (
( )的图像与
)的图像与 轴交于点
轴交于点 ,它的反函数
,它的反函数 的图像与
的图像与 轴交于点
轴交于点 ,并且这两个函数的图像交于点
,并且这两个函数的图像交于点 .若四边形
.若四边形 的面积是
的面积是 ,则
,则 ___________.
___________.
1已知函数 ,
, ,
, ,且
,且 ,
, .
.
(1)求 、
、 的解析式;
的解析式;
(2) 为定义在
为定义在 上的奇函数,且满足下列性质:①
上的奇函数,且满足下列性质:① 对一切实数
对一切实数 恒成立;②当
恒成立;②当 时
时 .
.
(ⅰ)求当 时,函数
时,函数 的解析式;
的解析式;
(ⅱ)求方程 在区间
在区间 上的解的个数.
上的解的个数.
设 的定义域为D,若
的定义域为D,若 满足下面两个条件,则称
满足下面两个条件,则称 为闭函数.①
为闭函数.① 在D内是单调函数;②存在
在D内是单调函数;②存在 ,使f(x)在[a,b]上的值域为[a,b].如果
,使f(x)在[a,b]上的值域为[a,b].如果 为闭函数,那么k的取值范围是
为闭函数,那么k的取值范围是
| A.k<l | B. |
C.k >-1 | D. |
定义在(-1,1)上的函数,f(x)满足:f(x)-f(y)=f(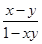 );当x∈(-1,0)时,有f(x)>0.若p=f(
);当x∈(-1,0)时,有f(x)>0.若p=f(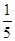 )+f(
)+f( ),Q=f(
),Q=f(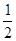 ),R=f(0);则 P,Q,R的大小关系为
),R=f(0);则 P,Q,R的大小关系为
| A.R>Q>P | B.R>P>Q | C.P>R>Q | D.Q>P>R |
试题篮
()