高中数学三面角、直三面角的基本性质试题

已知函数在R上满足则曲线在点
处的切线方程是 (     )

A．x-y-2=0

B．x-y=0

C．3x+y-2=0

D．3x-y-2="0"

（本小题满分16分）对于函数，如果存在实数使得
，那么称为的生成函数．
（Ⅰ）下面给出两组函数，是否分别为的生成函数？并说明理由；
第一组：；
第二组：；
（Ⅱ）设，生成函数．若不等式
在上有解，求实数的取值范围；
（Ⅲ）设，取，生成函数使 恒成立，求的取值范围．

（本小题满分16分） 已知函数，在处的
切线方程为．
（1）求的解析式；
（2）设，若对任意，总存在，使得
成立，求实数的取值范围．

（本小题满分15分） 一铁棒欲通过如图所示的直角走廊，试回答下列问题：

（1）求棒长L关于的函数关系式：；
（2）求能通过直角走廊的铁棒的长度的最大值．

设mÎN，若函数存在整数零点，则m的取值集合为        ．

某商场销售某种商品的经验表明，该商品每日的销售量y（单位：千克）与销售价格x（单位：元/千克）满足关系式，其中3＜x＜6，
a为常数，已知销售价格为5元/千克时，每日可售出该商品11千克．
（1）求a的值
（2）若该商品的成本为3元/千克，试确定销售价格x的值，使商场每日销售该商品所获得的利润最大．

．设函数f(x)＝－a＋x＋a，x∈(0,1]，a∈R^*.
(1)若f(x)在(0,1]上是增函数，求a的取值范围；
(2)求f(x)在(0,1]上的最大值．

设f(t)＝ ，那么＝________.

建造一间地面面积为12的背面靠墙的猪圈, 底面为长方形的猪圈正面的造价为120元/, 侧面的造价为80元/, 屋顶造价为1120元. 如果墙高3, 且不计猪圈背面的费用, 问怎样设计能使猪圈的总造价最低, 最低总造价是多少元?

如图为河岸一段的示意图，一游泳者站在河岸的A点处，欲前往河对岸的C点处。若河宽BC为100m，A、B相距100m，他希望尽快到达C，准备从A步行到E（E为河岸AB上的点），再从E游到C。已知此人步行速度为v，游泳速度为0.5v。
（I）设，试将此人按上述路线从A到C所需时间T表示为的函数；并求自变量 取值范围；
II）当为何值时，此人从A经E游到C所需时间T最小，其最小值是多少？

定义在R上的单调函数满足，且对任意都有

（I）试求的值并证明函数为奇函数；
（II）若对任意恒成立，求实数m的取值范围。

已知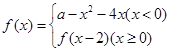，且函数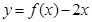恰有3个不同的零点，则实数a的取值范围是（   ）

A．[-4，0]

B．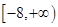

C．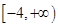

D．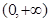

（本小题满分14分）某公司决定采用增加广告投入和技术改造投入两项措施来获得更大的收益．通过对市场的预测，当对两项投入都不大于3(百万元)时，每投入(百万元)广告费，增加的销售额可近似的用函数(百万元)来计算；每投入x(百万元)技术改造费用，增加的销售额可近似的用函数(百万元)来计算．现该公司准备共投入3(百万元)，分别用于广告投入和技术改造投入，请设计一种资金分配方案，使得该公司的销售额最大． (参考数据：≈1.41，≈1.73)

设若，则＝_________.

(本小题满分1 3分)
如图①，一条宽为l km的两平行河岸有村庄A和供电站C，村庄B与A、C的直线距离都是2km，BC与河岸垂直，垂足为D．现要修建电缆，从供电站C向村庄A、B供电．修建地下电缆、水下电缆的费用分别是2万元／km、4万元／km．
(Ⅰ)已知村庄A与B原来铺设有旧电缆仰，需要改造，旧电缆的改造费用是0.5万元／km．现
决定利用旧电缆修建供电线路，并要求水下电缆长度最短，试求该方案总施工费用的最小值．
(Ⅱ)如图②，点E在线段AD上，且铺设电缆的线路为CE、EA、EB．若∠DCE="θ" (0≤θ≤)，试用θ表示出总施工费用y(万元)的解析式，并求y的最小值．