(本小题满分12分)已知函数 ,
,
(1)若 时,
时, 在其定义域内单调递增,求
在其定义域内单调递增,求 的取值范围;
的取值范围;
(2)设函数 的图象
的图象 与函数
与函数 的图象
的图象 交于
交于 ,
, 两点,过线段
两点,过线段 的中点
的中点 作
作 轴的垂线分别交
轴的垂线分别交 、
、 于点
于点 ,
, ,问是否存在点
,问是否存在点 ,使
,使 在
在 处的切线与
处的切线与 在
在 处的切线平行?若存在,求
处的切线平行?若存在,求 的横坐标,若不存在,请说明理由。
的横坐标,若不存在,请说明理由。
已知函数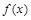 是以
是以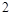 为周期的偶函数,当
为周期的偶函数,当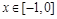 时,
时,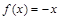 .若关于
.若关于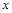 的方程
的方程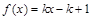 (
(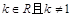 )在区间
)在区间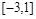 内有四个不同的实根,则
内有四个不同的实根,则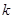 的取值范围是
的取值范围是
A. |
B.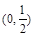 |
C.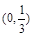 |
D. |
下列说法中:
①指数函数 的定义域为
的定义域为 ;②函数
;②函数 与函数
与函数 互为反函数;
互为反函数;
③空集是任何一个集合的真子集;④若 (
( 为常数),则函数
为常数),则函数 的最大值为
的最大值为 ;⑤函数
;⑤函数 的值域为
的值域为 .
.
正确的是 (请写出所有正确命题的序号).
(本题满分13分)设函数
 满足:
满足: 都有
都有 ,且
,且 时,
时, 取极小值
取极小值
(1) 的解析式;
的解析式;
(2)当 时,证明:函数图象上任意两点处的切线不可能互相垂直;
时,证明:函数图象上任意两点处的切线不可能互相垂直;
(3)设 , 当
, 当 时,求函数
时,求函数 的最小值,并指出当
的最小值,并指出当 取最小值时相应的
取最小值时相应的 值.
值.
函数y=f(x)的图象如图所示,则不等式f(x)<f(-x)+x的解集为______。
(本小题共12分)
已知函数 的图象过点
的图象过点 ,且在
,且在 内单调递减,在
内单调递减,在 上单调递增。
上单调递增。
(1)求 的解析式;
的解析式;
(2)若对于任意的 ,不等式
,不等式 恒成立,试问这样的
恒成立,试问这样的 是否存在.若存在,请求出
是否存在.若存在,请求出 的范围,若不存在,说明理由;
的范围,若不存在,说明理由;
试题篮
()