高中数学三面角、直三面角的基本性质试题

某工厂生产一种仪器的元件，由于受生产能力和技术水平的限制，会产生一些次品，根据经验知道，其次品率P与日产量x(万件)之间大体满足关系：(其中c为小于6的正常数)．  (注：次品率＝次品数/生产量，如P＝0.1表示每生产10件产品，有1件为次品，其余为合格品)，已知每生产1万件合格的元件可以盈利2万元，但每生产出1万件次品将亏损1万元，故厂方希望定出合适的日产量．
(1)试将生产这种仪器的元件每天的盈利额T(万元)表示为日产量x(万件)的函数；
(2)当日产量为多少时，可获得最大利润？

定义运算，函数图像的顶点是，且成等差数列，则    (    )

A．0

B．－14

C．－9

D．－3

养路处建造无底的圆锥形仓库用于贮藏食盐（供融化高速公路上的积雪之用），已建的仓库的底面直径为12米，高4米。养路处拟另建一个更大的圆锥形仓库，以存放更多食盐。现有两种方案：一是新建的仓库的底面直径比原来增加4米（高不变）；二是高度增加4米(底面直径不变)。
分别计算按这两种方案所建的仓库的体积；
分别计算按这两种方案所建的仓库的表面积；
哪个方案更经济些？

已知函数
（Ⅰ）当时, 求函数的单调增区间；
（Ⅱ）求函数在区间上的最小值；
（Ⅲ） 在（Ⅰ）的条件下，设,
证明：.参考数据：．

已知函数
⑴解不等式；
⑵若不等式的解集为空集，求的取值范围.

比较大小：        （填“＞”或“＜”）．

,若对任意，恒成立，则a的取值范围是________

若定义在R上的函数f(x)满足,且<0a="f" (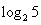),b="f" (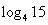),c="f" (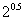)，则a,b,c的大小关系为

A．a>b>c

B．c>b>a

C．b>a>c

D．c>a>b

某造船公司年造船量是20艘，已知造船x艘的产值函数为R(x)=3700x+45x²-10x³（单位：万元），成本函数为C(x)=460x+5000（单位：万元），又在经济学中，函数f(x)的边际函数Mf(x)定义为Mf(x)=f(x+1)-f(x).
（1）求利润函数P(x)及边际利润函数MP(x)；（提示：利润=产值-成本）
（2）问年造船量安排多少艘时，可使公司造船的年利润最大？

已知函数．
（Ⅰ）解不等式: ；
（Ⅱ）若，求证：≤.

已知偶函数在上是增函数，则不等式的解集是          .

已知函数
（1）若不等式的解集为，求的取值范围；
（2）解关于的不等式；
（3）若不等式对一切恒成立，求的取值范围．

已知函数上的奇函数，且的图象关于直线x=1对称，当时，      ．

若动直线与函数与的图像分别交于两点，则的最大值为         ．

已知函数是定义在上的奇函数，若对于任意给定的不等实数、，不等式恒成立，则不等式的解集为          .