下列命题中正确的是( )
A.命题“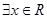 ,使得 ,使得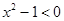 ”的否定是“ ”的否定是“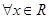 ,均有 ,均有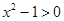 ”; ”; |
B.命题“若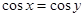 ,则x=y”的逆否命题是真命题: ,则x=y”的逆否命题是真命题: |
C.命题”若x=3,则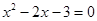 ”的否命题是“若 ”的否命题是“若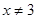 ,则 ,则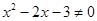 ”; ”; |
| D.命题“存在四边相等的四边形不是正方形”是假命题. |
定义在 上的函数
上的函数 ,其图象是连续不断的,如果存在非零常数
,其图象是连续不断的,如果存在非零常数 (
( ),使得对任意的
),使得对任意的 ,都有
,都有 ,则称
,则称 为“倍增函数”,
为“倍增函数”, 为“倍增系数”,
为“倍增系数”,
下列命题为真命题的是_ __(写出所有真命题对应的序号).
①若函数 是倍增系数
是倍增系数 的倍增函数,则
的倍增函数,则 至少有1个零点;
至少有1个零点;
②函数 是倍增函数,且倍增系数
是倍增函数,且倍增系数 ;
;
③函数 是倍增函数,且倍增系数
是倍增函数,且倍增系数 ;
;
④ .
.
对于定义域为[0,1]的函数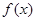 ,如果同时满足以下三个条件:
,如果同时满足以下三个条件:
①对任意的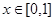 ,总有
,总有
②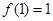
③若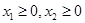 ,
, ,都有
,都有 成立;
成立;
则称函数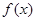 为理想函数. 下面有三个命题:
为理想函数. 下面有三个命题:
若函数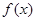 为理想函数,则
为理想函数,则 ;
;
函数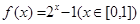 是理想函数;
是理想函数;
若函数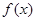 是理想函数,假定存在
是理想函数,假定存在 ,使得
,使得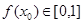 ,且
,且 ,则
,则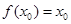 ;
;
其中正确的命题个数有( )
| A.3个 | B.2个 | C.1个 | D.0个 |
试题篮
()