高中数学截面及其作法选择题

设命题p：方程x²＋3x－1＝0的两根符号不同；命题q：方程x²＋3x－1＝0的两根之和为3，判断命题“Øp”、“Øq”、“p∧q”、“p∨q”为假命题的个数为（ ）

A．0

B．1

C．2

D．3

命题“∀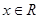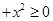，||”的否定是（   ）

A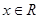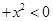．∀， ||	B．∀， ||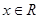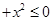
C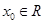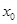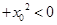．∃，||	D．∃，||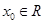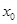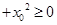

已知命题p:∀x∈R,2^x<3^x;命题q:∃x∈R,x³=1-x²,则下列命题中为真命题的是(　　)

A．p∧q

B．p∧q

C．p∧q

D．p∧q

不等式组的解集记为D，有下面四个命题：
p₁：∀（x，y）∈D，x＋2y≥－2，
p₂：∃（x，y）∈D，x＋2y≥2，
p₃：∀（x，y）∈D，x＋2y≤3，
p₄：∃（x，y）∈D，x＋2y≤－1．
其中的真命题是（ ）

A．p2，p3	B．p1，p2
C．p1，p4	D．p1，p3

已知命题p：“在△ABC中，若·＝·，则||＝||”，则在命题p的逆命题、否命题、逆否命题中，真命题的个数是(　　)

A．0	B．1
C．2	D．3

已知命题则是（   ）

A．	B．
C．	D．

给出下列命题：
①若给定命题p：∃x∈R，使得x²+x﹣1＜0，则¬p：∀x∈R，均有x²+x﹣1≥0；
②若p∧q为假命题，则p，q均为假命题；
③命题“若x²﹣3x+2=0，则x=2”的否命题为“若 x²﹣3x+2=0，则x≠2，
其中正确的命题序号是（ ）

A．①

B．①②

C．①③

D．②③

命题“，”的否定是（ ）

A．不存在，

B．，

C．，

D．，

“如果x、y∈R，且x²＋y²＝0，则x、y全为0”的否命题是（  ）

A．若x、y∈R且x^2＋y^2≠0，则x、y全不为0

B．若x、y∈R且x^2＋y^2≠0，则x、y不全为0

C．若x、y∈R且x、y全为0，则x^2＋y^2＝0

D．若x、y∈R且x、y不全为0，则x^2＋y^2≠0

命题：“若，则”的逆否命题是（   ）

A．若，则

B．若，则

C．若，则

D．若，则

给出下列命题中正确的是（     ）

A．棱柱被平面分成的两部分可以都是棱柱

B．底面是矩形的平行六面体是长方体

C．棱柱的底面一定是平行四边形

D．棱锥的底面一定是三角形

已知命题，则为（   ）

A．	B．
C．	D．

已知命题：函数在为增函数，：函数在为减函数，则在命题  和中，真命题是（   ）

A．

B．

C．

D．

【原题】下列说法中正确的是（     ）

A．若命题有，则有

B．若命题，则

C．若是的充分不必要条件，则是的必要不充分条件

D．方程有唯一解的充要条件是

已知命题:函数的最小正周期为；命题：若函数为偶函数，则关于对称.则下列命题是真命题的是（     ）

A．

B．

C．

D．