高中数学截面及其作法解答题

已知条件：
条件：
（Ⅰ）若,求实数的值；
（Ⅱ）若是的充分条件，求实数的取值范围.

命题：对任意实数都有恒成立；命题：关于的方程有实数根．若和有且只有一个为真命题，求实数的取值范围．

设命题：曲线上任一点处的切线的倾斜角都是锐角；命题：直线与曲线有两个不同的公共点；若命题和命题中有且只有一个是真命题，求实数的取值范围．

定义在R上的偶函数满足，且在[-3，-2]上是减函数，若是锐角三角形的两个内角，则与的大小关系为                 ；

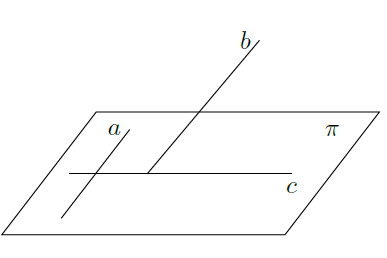
（1）如图，证明命题"a是平面 $\pi$内的一条直线，b是 $\pi$外的一条直线（b不垂直于 $\pi$），c是直线b在 $\pi$上的投影，若 $a\perp b$，则 $a\perp c$"为真。
（2）写出上述命题的逆命题，并判断其真假（不需要证明）

(本题满分12分)给出命题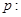方程表示焦点在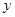轴上的椭圆；命题曲线与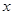轴交于不同的两点.
(1)在命题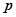中,求a的取值范围;
（2)如果命题“”为真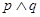，“”为假，求实数的取值范围．

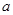（本小题满分14分）已知命题；命题，若且为真，求的取值范围.

已知命题p：方程x²＋mx＋1＝0有负实数根；
命题q：方程4x²＋4(m－2)x＋1＝0无实数根，
若“p或q”为真命题，“p且q”为假命题，求实数m的取值范围。

设命题p：函数是R上的减函数，命题q：函数f(x)＝x²－4x＋3在上的值域为[－1,3]，若“p且q”为假命题，“p或q”为真命题，求的取值范围．

已知函数，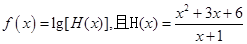
（1）求函数的定义域；
（2）求函数在区间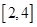上的最小值；
（3）已知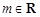，命题p：关于x的不等式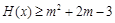对函数的定义域上的任意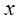恒成立；命题q：指数函数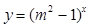是增函数．若“p或q”为真，“p且q”为假，求实数m的取值范围．

已知，设和是方程的两个根，不等式对任意实数恒成立；函数有两个不同的零点.求使“P且Q”为真命题的实数的取值范围.

命题方程有两个不等的正实数根， 命题方程无实数根。若“或”为真命题，求的取值范围。

命题：已知a、b为实数，若x²+ax+b≤0 有非空解集，则a²－ 4b≥0.写出该命题的逆命题、否命题、逆否命题，并判断这些命题的真假。

已知命题：方程所表示的曲线为焦点在x轴上的椭圆；命题：实数满足不等式＜０．
（1）若命题为真，求实数的取值范围；
（2）若命题是命题的充分不必要条件，求实数的取值范围

已知命题“若上是减函数”；“关于的不等式的解集为”．若“或”为真，求实数的取值范围．