如图,在三棱柱A1B1C1-ABC中,D,E,F分别是AB,AC,AA1的中点.设三棱锥F-ADE的体积为V1,三棱柱A1B1C1-ABC的体积为V2,则V1∶V2=________.
如图,在四棱锥P﹣ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.
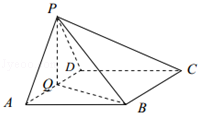
(1)若PA=PD,求证:平面PQB⊥平面PAD;
(2)若平面PAD⊥平面ABCD,且PA=PD=AD=2,点M在线段PC上,且PM=3MC,求三棱锥P﹣QBM的体积.
若三棱锥的三视图如图所示,则该三棱锥的体积为( )

|
A.80 B.40 C. D.
D.
(本小题满分12分)在四棱锥P-ABCD中,PC⊥平面ABCD,DC∥AB,DC=1,AB=4,BC=2 ,∠CBA=30°.
,∠CBA=30°.
(1)求证:AC⊥PB;
(2)当PD=2时,求此四棱锥的体积.
用与球心距离为2的平面去截球,所得的截面面积为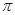 ,则球的体积为( )
,则球的体积为( )
A. |
B.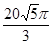 |
C.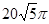 |
D.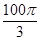 |
某四面体的三视图如图所示,该四面体四个面的面积中最大的是( )

| A.8 | B. |
C. |
D.10 |
已知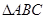 的三边长分别为
的三边长分别为 ,
, ,
, ,
, 是
是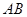 边上的点,
边上的点,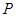 是平面
是平面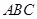 外一点,给出下列四个命题:
外一点,给出下列四个命题:
①若 平面
平面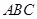 ,则三棱锥
,则三棱锥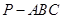 的四个面都是直角三角形;
的四个面都是直角三角形;
②若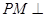 平面
平面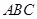 ,且
,且 是
是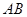 边的中点,则有
边的中点,则有 ;
;
③若 ,
,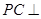 平面
平面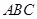 ,则
,则 面积的最小值为
面积的最小值为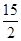 ;
;
④若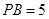 ,
,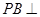 平面
平面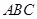 ,则三棱锥
,则三棱锥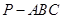 的外接球体积为
的外接球体积为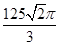 ;
;
其中正确命题的个数是( )
| A.1 | B.2 | C.3 | D.4 |
一个四面体的三视图如图所示,则该四面体的表面积是( )
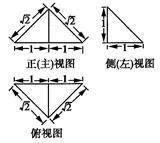
A. ] ] |
B.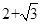 |
C.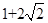 |
D.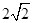 |
如图是一个几何体的三视图,其中正视图和侧视图都是一个两底长分别为2和4,腰长为4的等腰梯形,则该几何体的侧面积是
| A.6π | B.12π | C.18π | D.24π |
试题篮
()