高中数学选择题

已知数列{a_n}（n∈N^*）是各项均为正数且公比不等于1的等比数列，对于函数y=f（x），若数列{1nf（a_n）}为等差数列，则称函数f（x）为“保比差数列函数”．现有定义在（0，+∞）上的三个函数：①f（x）=；②f（x）=e^x   ③f（x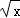）=，则为“保比差数列函数”的是（ ）

A．①②

B．②③

C．①③

D．①②③

某辆汽车购买时的费用是15万元，每年使用的保险费、路桥费、汽油费等约为1.5万 元．年维修保养费用第一年3000元，以后逐年递增3000元，则这辆汽车报废的最佳年 限（即使用多少年的年平均费用最少）是（ ）

A．8 年

B．1O 年

C．12 年

D．15 年

已知数列{a_n}是各项均为正数且公比不等于1的等比数列．对于函数y=f（x），若数列{lnf（a_n）}为等差数列，则称函数f（x）为“保比差数列函数”．现有定义在（0，+∞）上的如下函数：
①，
②f（x）=x²，
③f（x）=e^x，
④，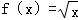
则为“保比差数列函数”的所有序号为（ ）

A．①②

B．③④

C．①②④

D．②③④

设a＞1，定义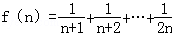，如果对任意的n∈N*且n≥2，不等式12f（n）+7log_ab＞7log_a+1b+7（a＞0且a≠1）恒成立，则实数b的取值范围是（ ）

A．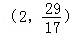

B．（0，1）

C．（0，4）

D．（1，+∞）

《莱因德纸草书》是世界上最古老的数学著作之一．书中有一道这样的题目：把100个面包分给五个人，使每人所得成等差数列，且使较大的三份之和的是较小的两份之和，问最小1份为（ ）

A．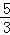

B．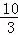

C．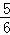

D．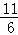

如图，以Ox为始边作任意角α，β，它们的终边与单位圆分别交于A，B点，则的值等于（ ）

A．sin（α+β）

B．sin（α﹣β）

C．cos（α+β）

D．cos（α﹣β）

已知角α的终边与单位圆相交于点P（sin，cos），则sinα=（ ）

A．﹣

B．﹣

C．

D．

设任意角α的终边与单位圆的交点为P₁（x，y），角α+θ的终边与单位圆的交点为P₂（y，﹣x），则下列说法中正确的是（ ）

A．sin（α+θ）=sinα	B．sin（α+θ）=﹣cosα
C．cos（α+θ）=﹣cosα	D．cos（α+θ）=﹣sinα

某中学进行模拟考试有80个考室，每个考室30个考生，每个考试座位号按1～30号随机抽取试卷进行评分标准，每个考场抽取座位号为15号考生试卷质检，这种抽样方法是（　　）

A．简单随机抽样

B．系统抽样

C．分层抽样

D．分组抽样

某防疫站对学生进行身体健康调查，欲采用分层抽样的办法抽取样本．某中学共有学生2000名，抽取了一个容量为200的样本，已知样本中女生比男生少6人，则该校共有女生（　　）

A．1030人

B．97人

C．950人

D．970人

某学校用分层抽样的方法从三个年级抽取若干学生，调查“马年春节”学生参加社会实践活动情况，有关数据如下（单位：人）：则x和y的值分别为（　　）

年级	年级人数	年级人数
高一	1080	x
高二	1350	y
高三	900	20

 
A.24，50    B.24，30    C.30，24    D.30，50

有一次青年志愿者联欢会上，到会的女青年比男青年多12人，从这些青年中随机挑选一人表演节目，若选到男青年的概率为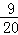，则参加联欢会的青年共有（　　）

A．120人

B．144人

C．240人

D．360人

某市有大型超市200家、中型超市400家、小型超市1400 家．为掌握各类超市的营业情况，现按分层抽样方法抽取一个容量为100的样本，应抽取中型超市（　　）

A．70家

B．50家

C．20家

D．10家

某学校要从高中的三个年级共1800名学生中用分层抽样的方法抽取一个样本对学生的社会实践活动进行统计分析，已知抽取的样本中三个年级学生（依次是一、二、三年级）人数的比例是5：4：3，则该学校高三年级的学生人数是（　　）

A．300

B．450

C．500

D．600

某商场有四类食品，食品类别和种数见下表：

类别	粮食类	植物油类	动物性食品类	果蔬类
种数	40	10	30	20

 
现从中抽取一个容量为20的样本进行食品安全检测．若采用分层抽样的方法抽取样本，则抽取的植物油类与果蔬类食品种数之和是（　　）
A.7    B.6    C.5    D.4