高中数学解答题

定义在非零实数集上的函数满足，且是区间上的递增函数. （1）求：的值；（2）求证：；（3）解不等式.

如图，在正方体ABCD-A₁B₁C₁D₁中，E、F、G分别是CB、CD、CC₁的中点，
求证：平面A B₁D₁∥平面EFG;
（2） 求证：平面AA₁C⊥面EFG.

(12分) 如图，已知△ABC是正三角形，EA、CD都垂直于平面ABC，且EA=AB=2a,DC=a,F是BE的中点，求证：(1)  FD∥平面ABC;  (2)  AF⊥平面EDB.

(12分) 已知△ABC三边所在直线方程为AB：3x+4y+12=0，BC：4x－3y+16=0，CA：2x+y－2=0，求AC边上的高所在的直线方程.

已知函数f(x)=log₂，(x∈(－∞，－)∪(，+∞))
（1）判断函数f(x)的奇偶性，并说明理由；
（2）判断函数f(x)在区间(，+∞)上的单调性．

求实数m的取值范围，使关于x的方程x²－2x＋m＋1＝0有两个正根．

已知A＝｛x| x²＋ax＋b＝0｝，B＝｛x| x²＋cx＋15＝0｝，A∪B＝｛3，5｝，A∩B＝｛3｝，求实数a，b，c的值

（本小题满分14分）
已知函数，．
（1）设（其中是的导函数），求的最大值；
（2）证明: 当时，求证：；
（3）设,当时,不等式恒成立,求的最大值．

（本小题满分12分）
将10个白小球中的3个染成红色，3个染成黄色，试解决下列问题：
求取出3个小球中红球个数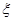的分布列和数学期望；
求取出3个小球中红球个数多于白球个数的概率.

（本小题满分12分）
在中，已知，
(1) 求的值；
(2) 若，求的面积；
(3) 若函数，求的值．

（本小题满分14分）
已知函数．
⑴若，求曲线在点处的切线方程；
⑵若函数在其定义域内为增函数，求正实数的取值范围；
⑶设函数，若在上至少存在一点，使得成立，求实数的取值范围．

（本小题满分12分）
已知椭圆：的离心率为，以原点为圆心，椭圆的短半轴长为半径的圆与直线相切．
⑴求椭圆C的方程；
⑵设，是椭圆上的点，连结交椭圆于另一点，求直线的斜率的取值范围．

（本小题满分12分）
某班级甲组有6名学生，其中有3名女生；乙组有6名学生，其中有2名女生．现采用分层抽样（层内采用不放回简单随即抽样）从甲、乙两组中共抽取4名学生进行社会实践活动．
（1）求从甲组抽取的学生中恰有1名女生的概率；
（2）求从乙组抽取的学生中至少有1名男生的概率；
（3）求抽取的4名学生中恰有2名女生的概率．   

设函数。
（1）当时，求函数的定义域；
（2）若函数的定义域为，试求的取值范围．

如图，已知中的两条角平分线和相交于，，在上，且。    
（1）证明：四点共圆；
（2）证明：平分。