如图,在四棱锥 中,底面
中,底面 为直角梯形,
为直角梯形,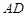 ∥
∥ ,
, ,平面
,平面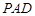 ⊥底面
⊥底面 ,
, 为
为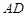 的中点,
的中点, 是棱
是棱 上的点,
上的点,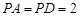 ,
, ,
, .
.
(Ⅰ)求证:平面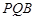 ⊥平面
⊥平面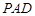 ;
;
(Ⅱ)若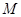 为棱
为棱 的中点,求异面直线
的中点,求异面直线 与
与 所成角的余弦值.
所成角的余弦值.
已知平面向量 ,
, ,
, ,其中
,其中 ,且函数
,且函数 的图象过点
的图象过点 .
.
(1)求 的值;
的值;
(2)将函数 图象上各点的横坐标变为原来的的2倍,纵坐标不变,得到函数
图象上各点的横坐标变为原来的的2倍,纵坐标不变,得到函数 的图象,求函数
的图象,求函数 在
在 上的最大值和最小值.
上的最大值和最小值.
解答下列问题:
(1)求平行于直线3x+4y 2=0,且与它的距离是1的直线方程;
(2)求垂直于直线x+3y 5=0且与点P( 1,0)的距离是 的直线方程.
的直线方程.
如图示,在底面为直角梯形的四棱椎P ABCD中,AD//BC,ÐABC= 900, PA^平面ABCD,PA= 4,AD= 2,AB=2 ,BC = 6.
,BC = 6.

(1)求证:BD^平面PAC ;
(2)求二面角A—PC—D的正切值;
(3)求点D到平面PBC的距离.
如图所示,在圆锥PO中, PO= ,ʘO的直径AB=2, C为弧AB的中点,D为AC的中点.
,ʘO的直径AB=2, C为弧AB的中点,D为AC的中点.

(1)求证:平面POD^平面PAC;
(2)求二面角B—PA—C的余弦值.
一个多面体的直观图、正视图、侧视图、俯视图如图所示,M、N分别为A1B、B1C1的中点.
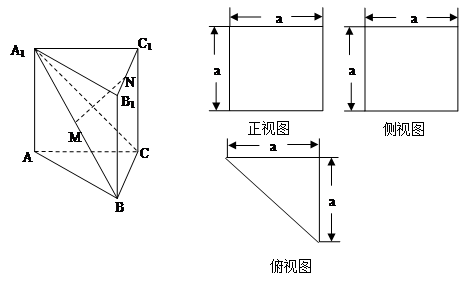
(1)求证:MN//平面ACC1A1;
(2)求证:MN^平面A1BC.
知椭圆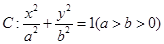 的离心率为
的离心率为 ,定点
,定点 ,椭圆短轴的端点是
,椭圆短轴的端点是 ,且
,且 .
.
(1)求椭圆 的方程;
的方程;
(2)设过点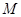 且斜率不为0的直线交椭圆
且斜率不为0的直线交椭圆 于
于 两点.试问
两点.试问 轴上是否存在异于
轴上是否存在异于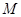 的定点
的定点 ,使
,使 平分
平分 ?若存在,求出点
?若存在,求出点 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
一个袋子里装有7个球,其中有红球4个, 编号分别为1,2,3,4;白球3个,编号分别为1,2,3.从袋子中任取4个球(假设取到任何一个球的可能性相同).
(Ⅰ)求取出的4个球中, 含有编号为3的球的概率;
(Ⅱ)在取出的4个球中, 红球编号的最大值设为X,求随机变量X的分布列和数学期望.
已知曲线 的参数方程为
的参数方程为 (
( 为参数),曲线
为参数),曲线 的极坐标方程
的极坐标方程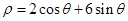 .
.
(Ⅰ)将曲线 的参数方程化为普通方程,将曲线
的参数方程化为普通方程,将曲线 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(Ⅱ)曲线 ,
, 是否相交,若相交请求出公共弦的长,若不相交,请说明理由.
是否相交,若相交请求出公共弦的长,若不相交,请说明理由.
试题篮
()