用 ,
, ,
, ,
, ,
, 这五个数字组成无重复数字的自然数.
这五个数字组成无重复数字的自然数.
(1)在组成的三位数中,求所有偶数的个数;
(2)在组成的三位数中,如果十位上的数字比百位上的数字和个位上的数字都小,则称这个数为“凹数”,如 ,
, 等都是“凹数”,试求“凹数”的个数;
等都是“凹数”,试求“凹数”的个数;
(3)在组成的五位数中,求恰有一个偶数数字夹在两个奇数数字之间的自然数的个数.
移动公司在国庆期间推出 套餐,对国庆节当日办理套餐的客户进行优惠,优惠方案如下:选择套餐一的客户可获得优惠200元,选择套餐二的客户可获得优惠500元,选择套餐三的客户可获得优惠300元,国庆节当天参与活动的人数统计结果如图所示,现将频率视为概率.
套餐,对国庆节当日办理套餐的客户进行优惠,优惠方案如下:选择套餐一的客户可获得优惠200元,选择套餐二的客户可获得优惠500元,选择套餐三的客户可获得优惠300元,国庆节当天参与活动的人数统计结果如图所示,现将频率视为概率.
(Ⅰ)求某人获得优惠金额不低于300元的概率;
(Ⅱ)若采用分层抽样的方式从参加活动的客户中选出6人,再从该6人中随机选两人,求这两人获得相等优惠金额的概率.
已知圆M的圆心M在x轴上,半径为1,直线 :y=
:y= x-
x- 被圆M所截的弦长为
被圆M所截的弦长为 ,且圆心M在直线
,且圆心M在直线 的下方.
的下方.
(1)求圆M的方程;
(2)设A(0,t),B(0,t+6)(-5≤t≤-2),若圆M是△ABC的内切圆,求△ABC的面积S的最大值和最小值.
某市政府为了确定一个较为合理的居民用电标准,必须先了解全市居民日常用电量的分布情况.现采用抽样调查的方式,获得了n位居民在2012年的月均用电量(单位:度)数据,样本统计结果如下图表:
| 分 组 |
频 数 |
频 率 |
| [0, 10) |
|
0.05 |
| [10,20) |
|
0.10 |
| [20,30) |
30 |
|
| [30,40) |
|
0.25 |
| [40,50) |
|
0.15 |
| [50,60] |
15 |
|
| 合 计 |
n |
1 |

(1)求月均用电量的中位数与平均数估计值;
(2)如果用分层抽样的方法从这n位居民中抽取8位居民,再从这8位居民中选2位居民,那么至少有1位居民月均用电量在30至40度的概率是多少?
(3)用样本估计总体,把频率视为概率,从这个城市随机抽取3位居民(看作有放回的抽样),求月均用电量在30至40度的居民数X的分布列.
一个盒子里装有三张卡片,分别标记有数字1,2,3,这三张卡片除标记的数字外完全相同.随机有放回地抽取3次,每次抽取1张,将抽取的卡片上的数字依次记为a,b,c.
(1)求“抽取的卡片上的数字满足a+b=c”的概率;
(2)求“抽取的卡片上的数字a,b,c不完全相同”的概率.
已知函数f(x)=xln x,g(x)=-x2+ax-2(e为自然对数的底数,a∈R).
(1)判断曲线y=f(x)在点(1,f(1))处的切线与曲线y=g(x)的公共点个数;
(2)当 时,若函数y=f(x)-g(x)有两个零点,求
时,若函数y=f(x)-g(x)有两个零点,求 的取值范围.
的取值范围.
选修4-4:坐标系与参数方程选讲
已知在直角坐标系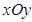 中,直线
中,直线 的参数方程为
的参数方程为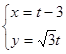 ,(
,(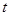 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,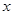 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线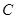 的极坐标方程为
的极坐标方程为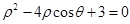 .
.
(Ⅰ)求直线 的普通方程和曲线
的普通方程和曲线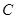 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设点 是曲线
是曲线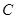 上的一个动点,求它到直线
上的一个动点,求它到直线 的距离
的距离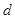 的取值范围.
的取值范围.
已知椭圆 的下顶点为P(0,-1),
的下顶点为P(0,-1), 到焦点的距离为
到焦点的距离为 .
.
(Ⅰ)设Q是椭圆上的动点,求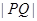 的最大值;
的最大值;
(Ⅱ)若直线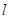 与圆O:x2+y2=1相切,并与椭圆
与圆O:x2+y2=1相切,并与椭圆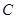 交于不同的两点A、B.当
交于不同的两点A、B.当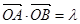 ,且满足
,且满足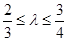 时,求
时,求 AOB面积S的取值范围.
AOB面积S的取值范围.
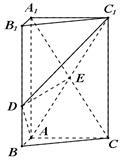
如图,三棱柱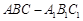 中,
中,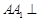 平面
平面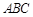 ,
,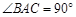 ,
,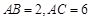 , 点
, 点 在线段
在线段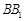 上,且
上,且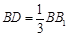 ,
, .
.
(Ⅰ)求证:直线 与平面
与平面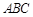 不平行;
不平行;
(Ⅱ)设平面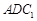 与平面
与平面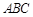 所成的锐二面角为
所成的锐二面角为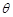 ,若
,若 ,求
,求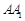 的长;
的长;
(Ⅲ)在(Ⅱ)的条件下,设平面 平面
平面 ,求直线
,求直线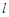 与
与 所成的角的余弦值.
所成的角的余弦值.
已知数列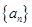 的前
的前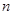 项和为
项和为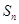 ,且
,且 .
.
(1)求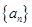 的通项公式;
的通项公式;
(2)设 ,若
,若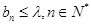 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)设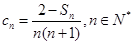 ,
, 是数列
是数列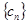 的前
的前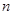 项和,证明
项和,证明 .
.
试题篮
()