销售甲、乙两种商品所得利润分别是 万元,它们与投入资金
万元,它们与投入资金 万元的关系分别为
万元的关系分别为 ,
, ,(其中m,a, b都为常数),函数
,(其中m,a, b都为常数),函数 对应的曲线C1、C2如图所示.
对应的曲线C1、C2如图所示.
(1)求函数 的解析式;
的解析式;
(2)若该商场一共投资4万元经销甲、乙两种商品,求该商场所获利润的最大值.
在直角坐标系中,圆 的参数方程
的参数方程 (
( 为参数).以
为参数).以 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(1)求曲线 的极坐标方程;
的极坐标方程;
(2)设直线 极坐标方程是
极坐标方程是 射线
射线 与圆
与圆 的交点为
的交点为 、
、 ,与直线
,与直线 的交点为
的交点为 ,求线段
,求线段 的长.
的长.
如图,在△ABC中已知∠B=60°, ,D是BC边上的一点.
,D是BC边上的一点.
(1)若AD=2,在△ACD的面积S= ,求CD的长.
,求CD的长.
(2)若AB=AD,试求△ACD面积S的最大值.
在四棱锥 中,
中, 平面
平面 ,底面
,底面 为直角梯形,
为直角梯形, ,
, ,
, 且
且 为
为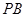 的中点.
的中点.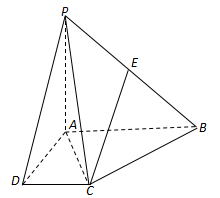
(1)求证: 平面
平面 ;
;
(2)求直线 与平面
与平面 所成角的正切值.
所成角的正切值.
已知函数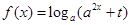 ,其中
,其中 且
且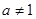 .
.
(1)当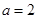 时,若
时,若 无解,求
无解,求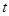 的范围;
的范围;
(2)若存在实数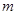 ,
, (
(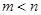 ),使得
),使得 时,函数
时,函数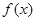 的值域都也为
的值域都也为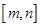 ,求
,求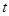 的范围.
的范围.
试题篮
()