高中数学解答题

设等差数列{a_n}的公差为d，点(a_n，b_n)在函数f (x)＝2^x的图象上(n∈N^*)．
（Ⅰ）证明：数列{b_n}为等比数列；
（Ⅱ）若a₁＝1，直线y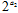＝(ln2)(x－a₂)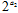＋在x轴上的截距为2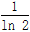－，求数列{a_nb}的前n项和S_n.

已知抛物线与双曲线有公共焦点，点是曲线在第一象限的交点，且．
（Ⅰ）求双曲线的方程；
（Ⅱ）以双曲线的另一焦点为圆心的圆与直线相切，圆．过点作互相垂直且分别与圆、圆相交的直线和，设被圆截得的弦长为，被圆截得的弦长为，问：是否为定值？如果是，请求出这个定值；如果不是，请说明理由．

如图，在四棱锥中，侧面PAD⊥底面ABCD，侧棱，，底面为直角梯形，其中BC∥AD，AB⊥AD，，O为AD中点．

（Ⅰ）求直线与平面所成角的余弦值；
（Ⅱ）线段上是否存在一点，使得二面角的余弦值为？若存在，求出的值；若不存在，请说明理由．

设函数其中是的导函数．
（1）令，猜测的表达式并给予证明；
（2）若恒成立，求实数的取值范围；
（3）设，比较与的大小，并说明理由．

如图，已知椭圆C的方程为，双曲线的两条渐近线为，过椭圆C的右焦点F作直线，使交于点P，设与椭圆C的两个焦点由上至下依次为A，B．

（1）若的夹角为60，且双曲线的焦距为4，求椭圆C的方程；
（2）若,求椭圆C的离心率．

已知正的边长为4，CD是AB边上的高，E,F分别是AC和BC边上的中点，现将沿CD翻折成直二面角A-BC-B．

（1）求二面角E-DF-C的余弦值；
（2）在线段BC上是否存在一点P，使APDE?如果存在，求出的值；如果不存在，说明理由．

已知数列的前项和与通项满足．
（1）求数列的通项公式；
（2）数列满足，求证：．

设，是否存在关于自然数n的函数，使等式对于的一切自然数都成立？并证明你的结论．

已知椭圆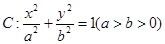，直线(m+3)x+(1-2m)y-m-3=0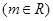恒过的定点F为椭圆的一个焦点，且椭圆上的点到焦点F的最大距离为3．
（1）求椭圆C的方程；
（2）若直线MN为垂直于x轴的动弦，且M，N均在椭圆C上，定点T(4,0)，直线MF与直线NT交于点S．
①证：点S恒在椭圆C上；
②求△MST面积的最大值．

在平面直角坐标系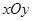中，过定点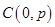作直线与抛物线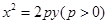相交于A，B两点．

（1）若点N是点C关于坐标原点O的对称点，求△ANB面积的最小值；
（2）是否存在垂直于y轴的直线l，使得l被以AC为直径的圆截得的弦长恒为定值？若存在，求出l的
方程；若不存在，说明理由．

将圆上每一点的横坐标都伸长为原来的倍，纵坐标都伸长为原
来的2倍，得到曲线C．
（1）求曲线C的参数方程；
（2）以坐标原点为极点，x轴正半轴为极轴建立极坐标系，已知点P的极坐标为，且点P关于直线的对称点为点Q，设直线PQ与曲线C相交于A、B两点，求线段AB的垂直平分线的极坐标方程．

已知三点、、．
（1）求以，为焦点且过点P的椭圆的标准方程；
（2）设点P、、关于直线y=x的对称点分别为、、，求以、为焦点且过点的双
曲线的标准方程．

我们把一系列向量按次序排成一列，称之为向量列，记作，已知向量列满足：，．
（1）证明：数列是等比数列；
（2）设表示向量与间的夹角，若，对于任意正整数，不等式恒成立，求实数的范围；
（3）设，问数列中是否存在最小项？若存在，求出最小项；若不存在，请说明理由．

袋子中放有大小和形状相同的小球若干，其中标号为1的小球1个，标号为2的小球2个，标号为3的小球个，已知从袋中随机抽取1个小球，取到标号3的小球的概率为．
（1）求的值；
（2）从袋子中不放回地随机抽取2个球，记第一次取出的小球标号为，第二次取出的小球标号为．
①记“”为事件A，求事件A的概率；
②在区间内任取2个实数，求事件“” 恒成立的概率．

对某电子元件进行寿命追踪调查，所得情况如右频率分布直方图．

（1）图中纵坐标处刻度不清，根据图表所提供的数据还原；
（2）根据图表的数据按分层抽样，抽取个元件，寿命为之间的应抽取几个；
（3）从（2）中抽出的寿命落在之间的元件中任取个元件，求事件“恰好有一个寿命为，一个寿命为”的概率．