高中数学解答题

如图，直三棱柱ABC﹣A ₁B ₁C ₁的底面为直角三角形，两直角边AB和AC的长分别为4和2，侧棱AA ₁的长为5．

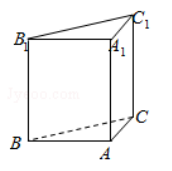
（1）求三棱柱ABC﹣A ₁B ₁C ₁的体积；    

（2）设M是BC中点，求直线A ₁M与平面ABC所成角的大小.

已知一个口袋有 $m$个白球， $n$个黑球 $（m，n\in N^{*}\mathit{ }，\mathit{n}\ge 2）$ ，这些球除颜色外全部相同．现将口袋中的球随机的逐个取出，并放入如图所示的编号为1，2，3，…， $m+n$ 的抽屉内，其中第k次取出的球放入编号为k的抽屉 $（k=1，2，3，\dots ，m+n）$ ．

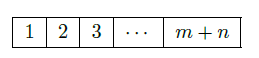
（Ⅰ）试求编号为2的抽屉内放的是黑球的概率 $p$；

（Ⅱ）随机变量x表示最后一个取出的黑球所在抽屉编号的倒数， $E（X）$ 是 $X$ 的数学期望，证明 $E（X\mathit{）＜}\frac{n}{(m+n)(n-1)}$ ．

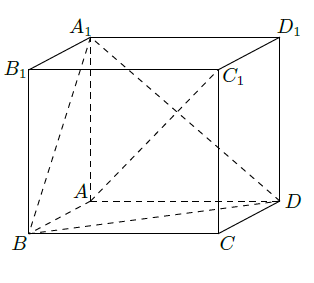
如图，在平行六面体 $\mathit{ABCD}﹣A_1{B}_1{C}_1{D}_1$ 中， $A{A}_1\perp \mathit{平面}\mathit{ABCD}$ ，且 $\mathit{AB}=\mathit{AD}=2$ ， $A{A}_1=\sqrt{3}$ ， $\angle \mathit{BAD}=120°$ ．

（Ⅰ）求异面直线 $A_{1}B$ 与 $A{C}_1$ 所成角的余弦值；

（Ⅱ）求二面角 $B﹣A_{1}D﹣A$ 的正弦值．

已知a，b，c，d为实数，且 $a^2+b^2=4$ ， $c^2+d^2=16$ ，证明 $\mathit{ac}+\mathit{bd}\le 8$ ．

在平面直角坐标系 $\mathit{xOy}$ 中，已知直线l的参数方程为 $\left\{\begin{array}{c}x=-8+t\\ y=\frac{t}{2}\end{array}\right.$ （t为参数），曲线C的参数方程为 $\left\{\begin{array}{c}x=2s^2\\ y=2\sqrt{2}s\end{array}\right.$ （s为参数）．设P为曲线C上的动点，求点P到直线l的距离的最小值．

已知矩阵 $A=\left[\begin{array}{cc}0& 1\\ 1& 0\end{array}\right]$ ， $B=\left[\begin{array}{cc}1& 0\\ 0& 2\end{array}\right]$ ．

（Ⅰ）求AB；

（Ⅱ）若曲线C ₁： $\frac{x^2}{8}+\frac{y^2}{2}$ =1在矩阵AB对应的变换作用下得到另一曲线C ₂ ， 求C ₂的方程．

如图， $AB$为半圆 $O$的直径，直线 $PC$切半圆 $O$于点 $C$， $\mathit{AP}\perp \mathit{PC}$ ， $P$为垂足．

求证：（Ⅰ） $\angle \mathit{PAC}=\angle \mathit{CAB}$ ；

（Ⅱ） ${\mathit{AC}}^2=\mathit{AP}•\mathit{AB}$ ．

已知函数 $f（x）=x^3+a{x}^2+\mathit{bx}+1（a＞0，b\in R）$ 有极值，且导函数 $f\text{'}（x）$ 的极值点是 $f（x）$ 的零点．（极值点是指函数取极值时对应的自变量的值）

（Ⅰ）求b关于a的函数关系式，并写出定义域；

（Ⅱ）证明： $b^2＞3a$ ；

（Ⅲ）若 $f（x）$ ， $f\text{'}（x）$ 这两个函数的所有极值之和不小于 $﹣\frac{7}{2}$ ，求a的取值范围．

对于给定的正整数k，若数列 $\left\{a_n\right\}$ 满足： $a_{n-k}+a_{n-k+1}+\dots +a_{n-1}+a_{n+1}+\dots a_{n+k-1}+a_{n+k}=2k{a}_n$ 对任意正整数 $n（n＞k）$ 总成立，则称数列{a _n}是" $P（k）$ 数列"．

（Ⅰ）证明：等差数列 $\left\{a_n\right\}$ 是" $P（3）$ 数列"；

（Ⅱ）若数列 $\left\{a_n\right\}$ 既是"P（2）数列"，又是" $P（3）$ 数列"，证明： $\left\{a_n\right\}$ 是等差数列．

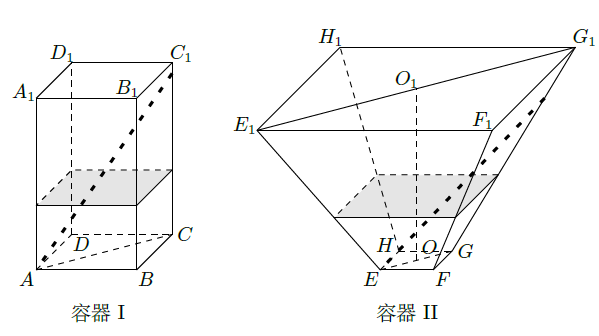
如图，水平放置的正四棱柱形玻璃容器 $Ⅰ$和正四棱台形玻璃容器 $Ⅱ$的高均为 $32cm$，容器 $Ⅰ$的底面对角线 $AC$的长为 $10\sqrt{7}$ cm，容器 $Ⅱ$的两底面对角线 $EG$， $E{ }_1{G}_{ 1}$的长分别为 $14cm$和 $62cm$．分别在容器 $Ⅰ$和容器 $Ⅱ$中注入水，水深均为 $12cm$．现有一根玻璃棒 $l$，其长度为 $40cm$．（容器厚度、玻璃棒粗细均忽略不计）

（Ⅰ）将l放在容器 $Ⅰ$中， $l$的一端置于点 $A$处，另一端置于侧棱 $CC{ }_1$上，求 $l$没入水中部分的长度；

（Ⅱ）将l放在容器 $Ⅱ$中， $l$的一端置于点 $E$处，另一端置于侧棱 $G{G}_{ 1}$上，求 $l$没入水中部分的长度．

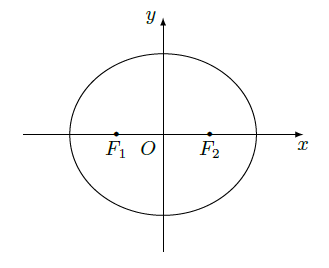
如图，在平面直角坐标系 $xOy$中，椭圆 $E：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$ 的左、右焦点分别为 $F{ }_1$， $F_{ 2}$， 离心率为 $\frac{1}{2}$ ，两准线之间的距离为 $8$．点P在椭圆E上，且位于第一象限，过点 $F_{ 1}$作直线 $P{F}_{ 1}$的垂线 $l{ }_1$， 过点 $F_{ 2}$作直线 $PF{ }_2$的垂线 $l{ }_2$．

（Ⅰ）求椭圆E的标准方程；

（Ⅱ）若直线 $l{ }_1$， $l 2$的交点Q在椭圆E上，求点P的坐标．

已知向量 $\vec{a}=（\mathit{cosx}，\mathit{sinx}）$ ， $\vec{b}=（3\mathit{，﹣}\sqrt{3}$ ）， $x\in \left[0，\pi \right]$ ．

（Ⅰ）若 $\vec{a}\parallel \vec{b}$ ，求x的值；

（Ⅱ）记 $f（x）=\vec{a}\cdot \vec{b}$ ，求 $f（x）$ 的最大值和最小值以及对应的x的值．

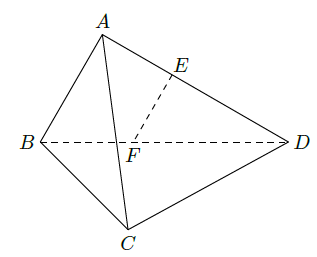
如图，在三棱锥 $A﹣\mathit{BCD}$ 中， $\mathit{AB}\perp \mathit{AD}$ ， $\mathit{BC}\perp \mathit{BD}$ ，平面 $\mathit{ABD}\perp$ 平面BCD，点E、F（E与A、D不重合）分别在棱AD，BD上，且 $\mathit{EF}\perp \mathit{AD}$ ．

求证：（Ⅰ）EF∥平面ABC；

（Ⅱ） $\mathit{AD}\perp \mathit{AC}$ ．

[选修4-5：不等式选讲]

已知函数 $f（x）=–x^2+\mathit{ax}+4，g\left(x\right)=\mathit{│x}+1│+\mathit{│x–}1│$ .

（1）当 $a=1$ 时，求不等式 $f（x）\ge g（x）$ 的解集；

（2）若不等式 $f（x）\ge g（x）$ 的解集包含 $\left[–1，1\right]$ ，求 a的取值范围.

[选修4―4：坐标系与参数方程]

在直角坐标系 $\mathit{xOy}$ 中，曲线 C的参数方程为 $\left\{\begin{array}{c}x=3\mathit{cos}\theta ,\\ y=\mathit{sin}\theta ,\end{array}\right.$ （ θ为参数），直线 l的参数方程为

$\left\{\begin{array}{c}x=a+4t,\\ y=1-t,\end{array}\right.（t\mathit{为参数）}$ .

（1）若 $a=-1$ ，求 C与 l的交点坐标；

（2）若 C上的点到 l的距离的最大值为 $\sqrt{17}$ ，求a.