设 是椭圆
是椭圆 上的两点,已知向量
上的两点,已知向量 ,若
,若 且椭圆的离心率
且椭圆的离心率 ,短轴长为2,O为坐标原点.
,短轴长为2,O为坐标原点.
(Ⅰ) 求椭圆的方程;
(Ⅱ)若直线AB过椭圆的焦点F(0,c),(c为半焦距),求直线AB的斜率k的值;
(Ⅲ)试问:△AOB的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
已知椭圆 :
: 的离心率为
的离心率为 ,其长轴长与短轴长的和等于6.
,其长轴长与短轴长的和等于6.
(1)求椭圆 的方程;
的方程;
(2)如图,设椭圆 的上、下顶点分别为
的上、下顶点分别为 ,
, ,
, 是椭圆上异于
是椭圆上异于 ,
, 的任意一点,直线
的任意一点,直线 ,
, 分别交
分别交 轴于点
轴于点 ,
, ,若直线
,若直线 与过点
与过点 ,
, 的圆
的圆 相切,切点为
相切,切点为 ,证明:线段
,证明:线段 的长为定值.
的长为定值.
若存在实常数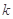 和
和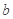 ,使得函数
,使得函数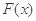 和
和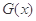 对其公共定义域上的任意实数
对其公共定义域上的任意实数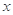 都满足:
都满足: 和
和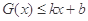 恒成立,则称此直线
恒成立,则称此直线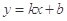 为
为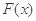 和
和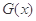 的“隔离直线”,已知函数
的“隔离直线”,已知函数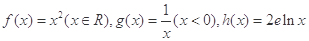 ,有下列命题:
,有下列命题:
①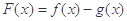 在
在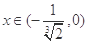 内单调递增;
内单调递增;
②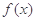 和
和 之间存在“隔离直线”,且
之间存在“隔离直线”,且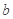 的最小值为
的最小值为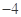 ;
;
③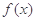 和
和 之间存在“隔离直线”,且
之间存在“隔离直线”,且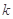 的取值范围是
的取值范围是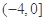 ;
;
④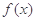 和
和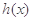 之间存在唯一的“隔离直线”
之间存在唯一的“隔离直线”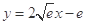 .
.
其中真命题的个数有( )
A.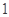 个 个 |
B.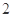 个 个 |
C.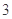 个 个 |
D.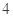 个 个 |
(本小题满分12分)如图,椭圆
 (
( )经过点
)经过点 ,离心率
,离心率 .
.
(1)求椭圆 的方程;
的方程;
(2)设直线 与椭圆
与椭圆 交于
交于 ,
, 两点,点
两点,点 关于
关于 轴的对称点为
轴的对称点为 (
( 与
与 不重合),则直线
不重合),则直线 与
与 轴是否交于一个定点?若是,请写出定点坐标,并证明你的结论;若不是,请说明理由.
轴是否交于一个定点?若是,请写出定点坐标,并证明你的结论;若不是,请说明理由.
(本小题满分12分)如图, 轴,点
轴,点 在
在 的延长线上,且
的延长线上,且 ,当点
,当点 在圆
在圆 上运动时.
上运动时.
(Ⅰ)求点 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ)过点 作圆
作圆 的切线
的切线 交曲线
交曲线 于
于 ,
, 两点,求
两点,求 面积
面积 的最大值和相应的点
的最大值和相应的点 的坐标.
的坐标.
(本小题满分12分)已知椭圆 ,其中
,其中 为左、右焦点,且离心率
为左、右焦点,且离心率 ,直线
,直线 与椭圆交于两不同点
与椭圆交于两不同点 .当直线
.当直线 过椭圆
过椭圆 右焦点
右焦点 且倾斜角为
且倾斜角为 时,原点
时,原点 到直线
到直线 的距离为
的距离为 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)若 ,当
,当 面积为
面积为 时,求
时,求 的最大值.
的最大值.
(本小题12分)已知椭圆 的右焦点为
的右焦点为 ,点
,点 在椭圆上.
在椭圆上.
(Ⅰ)求椭圆的离心率;
(Ⅱ)点 在圆
在圆 上,且
上,且 在第一象限,过
在第一象限,过 作圆
作圆 的切线交椭圆于
的切线交椭圆于 ,
, 两点,求证:△
两点,求证:△ 的周长是定值.
的周长是定值.
(本小题满分12分)已知函数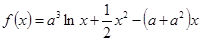
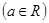 ,
,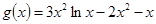 .
.
(1)判断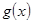 在区间
在区间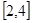 上单调性;
上单调性;
(2)若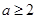 ,函数
,函数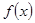 在区间
在区间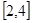 上的最大值为
上的最大值为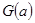 ,求
,求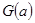 的解析式,并判断
的解析式,并判断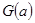 是否有最大值和最小值,请说明理由(参考数据:
是否有最大值和最小值,请说明理由(参考数据: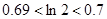 ).
).
(本小题满分12分)已知函数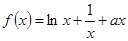 .
.
(1)若函数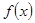 在
在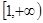 上是单调函数,求实数
上是单调函数,求实数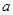 的取值范围;
的取值范围;
(2)已知函数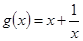 ,对于任意
,对于任意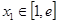 ,总存在
,总存在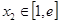 ,使得
,使得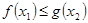 成立,求正实数
成立,求正实数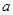 的取值范围.
的取值范围.
已知椭圆
 的左焦点为
的左焦点为 ,右焦点为
,右焦点为 ,离心率
,离心率 .过
.过 的直线交椭圆于
的直线交椭圆于 、
、 两点,且
两点,且 的周长为
的周长为 .
.
(1)求椭圆 的方程;
的方程;
(2)设动直线 与椭圆
与椭圆 有且只有一个公共点
有且只有一个公共点 ,且与直线
,且与直线 相交于点
相交于点 .求证:以
.求证:以 为直径的圆恒过一定点
为直径的圆恒过一定点 .并求出点
.并求出点 的坐标.
的坐标.
试题篮
()