(本小题满分14分)已知函数 .
.
(Ⅰ)若 ,关于
,关于 的不等式
的不等式 在区间
在区间 上恒成立,求
上恒成立,求 的取值范围;
的取值范围;
(Ⅱ)若 ,解关于
,解关于 的不等式
的不等式 ;
;
(Ⅲ)若 ,且
,且 ,求
,求 的取值范围.
的取值范围.
在钝角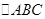 中,
中,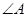 为钝角,令
为钝角,令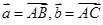 ,若
,若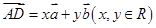 .现给出下面结论:
.现给出下面结论:
①当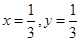 时,点
时,点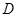 是
是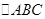 的重心;
的重心;
②记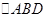 ,
,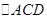 的面积分别为
的面积分别为 ,
,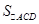 ,当
,当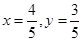 时,
时, ;
;
③若点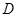 在
在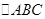 内部(不含边界),则
内部(不含边界),则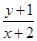 的取值范围是
的取值范围是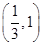 ;
;
④若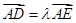 ,其中点
,其中点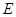 在直线
在直线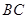 上,则当
上,则当 时,
时,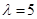 .
.
其中正确的有 (写出所有正确结论的序号)
(本小题满分12分)设各项均为正数的等比数列 中,
中,

(1)求数列 的通项公式;
的通项公式;
(2)若 ,求证:
,求证:  ;
;
(3)是否存在正整数 ,使得
,使得 对任意正整数
对任意正整数 均成立?若存在,求出
均成立?若存在,求出 的最大值,若不存在,说明理由.
的最大值,若不存在,说明理由.
在钝角△ABC中,∠A为钝角,令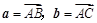 ,若
,若 .现给出下面结论:
.现给出下面结论:
①当 时,点D是△ABC的重心;
时,点D是△ABC的重心;
②记△ABD,△ACD的面积分别为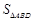 ,
,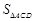 ,当
,当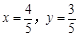 时,
时,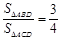 ;
;
③若点D在△ABC内部(不含边界),则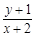 的取值范围是
的取值范围是 ;
;
④若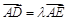 ,其中点E在直线BC上,则当
,其中点E在直线BC上,则当 时,
时,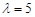 .
.
其中正确的有 (写出所有正确结论的序号).
(本小题满分14分)下面的茎叶图记录了甲、乙两代表队各10名同学在一次英语听力比赛中的成绩(单位:分).已知甲代表队数据的中位数为76,乙代表队数据的平均数是75.
(1)求 ,
, 的值;
的值;
(2)若分别从甲、乙两队随机各抽取1名成绩不低于80分的学生,求抽到的学生中,甲队学生成绩不低于乙队学生成绩的概率;
(3)判断甲、乙两队谁的成绩更稳定,并说明理由(方差较小者稳定).
(本小题满分12分)我们把一系列向量 按次序排成一列,称之为向量列,记作
按次序排成一列,称之为向量列,记作 ,已知向量列
,已知向量列 满足:
满足: ,
,
 .
.
(1)证明:数列 是等比数列;
是等比数列;
(2)设 表示向量
表示向量 与
与 间的夹角,若
间的夹角,若 ,对于任意正整数
,对于任意正整数 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的范围
的范围
(3)设 ,问数列
,问数列 中是否存在最小项?若存在,求出最小项;若不存在,请说明理由
中是否存在最小项?若存在,求出最小项;若不存在,请说明理由
如图,将平面直角坐标系中的纵轴绕原点 顺时针旋转
顺时针旋转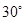 后,构成一个斜坐标平面
后,构成一个斜坐标平面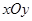 .在此斜坐标平面
.在此斜坐标平面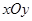 中,点
中,点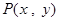 的 坐标定义如下:过点
的 坐标定义如下:过点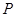 作两坐标轴的平行线,分别交两轴于
作两坐标轴的平行线,分别交两轴于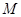 、
、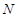 两点,则
两点,则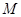 在
在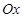 轴上表示的数为
轴上表示的数为 ,
,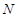 在
在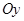 轴上表示的数为
轴上表示的数为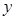 .那么以原点
.那么以原点 为圆心的单位圆在此斜坐标系下的方程为
为圆心的单位圆在此斜坐标系下的方程为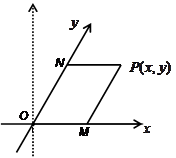
A.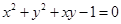 |
B.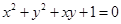 |
C.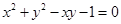 |
D.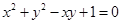 |
甲、乙两地相距1000 ,货车从甲地匀速行驶到乙地,速度不得超过80
,货车从甲地匀速行驶到乙地,速度不得超过80 ,已知货车每小时的运输成本(单位:元)由可变成本和固定成本组成,可变成本是速度平方的
,已知货车每小时的运输成本(单位:元)由可变成本和固定成本组成,可变成本是速度平方的 倍,固定成本为
倍,固定成本为 元.
元.
(Ⅰ)将全程运输成本 (元)表示为速度
(元)表示为速度 (
( )的函数,并指出这个函数的定义域;
)的函数,并指出这个函数的定义域;
(Ⅱ)为了使全程运输成本最小,货车应以多大的速度行驶?
(本小题满分14分)平面内一动点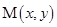 到定点
到定点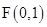 和到定直线
和到定直线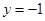 的距离相等,设
的距离相等,设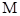 的轨迹是曲线
的轨迹是曲线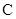 .
.
(1)求曲线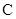 的方程;
的方程;
(2)在曲线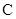 上找一点
上找一点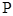 ,使得点
,使得点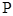 到直线
到直线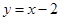 的距离最短,求出
的距离最短,求出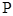 点的坐标;
点的坐标;
(3)设直线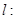
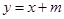 ,问当实数
,问当实数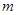 为何值时,直线
为何值时,直线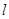 与曲线
与曲线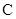 有交点?
有交点?
(本小题满分12分)已知 ,其中
,其中 均为实数,
均为实数,
(Ⅰ)求 的极值;
的极值;
(Ⅱ)设 ,
,
求证:对 恒成立;
恒成立;
(Ⅲ)设 ,若对
,若对 给定的
给定的 ,在区间
,在区间 上总存在
上总存在 使得
使得 成立,求m的取值范围.
成立,求m的取值范围.
(本小题满分12分)已知向量 ,
, ,函数
,函数 ,
, .
.
(Ⅰ)求函数 的图像的对称中心坐标;
的图像的对称中心坐标;
(Ⅱ)将函数 图像向下平移
图像向下平移 个单位,再向左平移
个单位,再向左平移 个单位得函数
个单位得函数 的图像,试写出
的图像,试写出 的解析式并作出它在
的解析式并作出它在 上的图像.
上的图像.
试题篮
()