设 为奇函数,
为奇函数, 为常数.
为常数.
(Ⅰ)求 的值;
的值;
(Ⅱ)判断 在区间(1,+∞)的单调性,并说明理由;
在区间(1,+∞)的单调性,并说明理由;
(Ⅲ)若对于区间[3,4]上的每一个 值,不等式
值,不等式 >
> 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
如图,在四棱锥 中,
中, ,
, 平面
平面 ,
, 平面
平面 ,
, ,
, ,
, .
.
(Ⅰ)求棱锥 的体积;
的体积;
(Ⅱ)求证:平面
 平面
平面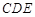 ;
;
(Ⅲ)在线段 上是否存在一点
上是否存在一点 ,使
,使 平面
平面 ?若存在,求出
?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
选修4-4:坐标系与参数方程
在直角坐标系 中,设倾斜角为
中,设倾斜角为 的直线
的直线 :
: ,(
,( 为参数)与曲线
为参数)与曲线 ,(
,( 为参数)相交于不同两点
为参数)相交于不同两点 、
、 .
.
(Ⅰ)若 ,求线段
,求线段 中点
中点 的坐标;
的坐标;
(Ⅱ)若 ,其中
,其中 ,求直线
,求直线 的斜率.
的斜率.
如图,在三棱锥 中,
中, ,
, ,
, °,平面
°,平面 平面
平面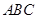 ,
, 、
、 分别为
分别为 、
、 中点.
中点.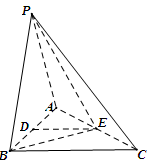
(1)求证: ;
;
(2)求二面角 的大小.
的大小.
某中学调查了某班全部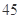 名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)
名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)
(1)从该班随机选 名同学,求该同学至少参加上述一个社团的概率;
名同学,求该同学至少参加上述一个社团的概率;
(2)在既参加书法社团又参加演讲社团的 名同学中,有5名男同学
名同学中,有5名男同学
 名女同学
名女同学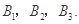 现从这
现从这 名男同学和
名男同学和 名女同学中各随机选
名女同学中各随机选 人,求
人,求 被选中且
被选中且 未被选中的概率.
未被选中的概率.
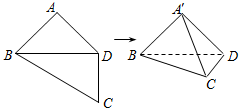
如图所示,在四边形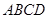 中,
中,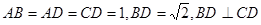 ,将四边形
,将四边形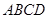 沿对角线
沿对角线 折成四面体
折成四面体 ,使平面
,使平面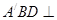 平面
平面 ,则下列结论正确的是 .
,则下列结论正确的是 .
(1)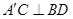 ;
;
(2)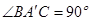 ;
;
(3) 与平面
与平面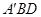 所成的角为
所成的角为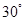 ;
;
(4)四面体 的体积为
的体积为 .
.
某市举行了“高速公路免费政策”满意度测评,共有1万人参加了这次测评(满分100分,得分全为整数).为了解本次测评分数情况,从中随机抽取了部分人的测评分数进行统计,整理见下表:
| 组别 |
分组 |
频数 |
频率 |
| 1 |
 |
60 |
0.12 |
| 2 |
 |
120 |
0.24 |
| 3 |
 |
180 |
0.36 |
| 4 |
 |
130 |
c |
| 5 |
 |
a |
0.02 |
| 合计 |
b |
1.00 |
(1)求出表中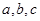 的值;
的值;
(2)若分数在(含60分)的人对“高速公路免费政策”表示满意,现从全市参加了这次满意度测评的人中随机抽取一人,求此人满意的概率;
(3)请你估计全市的平均分数.
已知 .
.
(1)求 的单调区间;
的单调区间;
(2)令 ,则
,则 时有两个不同的根,求
时有两个不同的根,求 的取值范围;
的取值范围;
(3)存在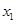 ,
,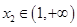 且
且 ,使
,使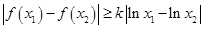 成立,求
成立,求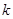 的取值范围.
的取值范围.
设函数 ,
,
(Ⅰ)求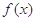 的最大值,并写出使
的最大值,并写出使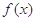 取最大值时x的集合;
取最大值时x的集合;
(Ⅱ)已知 中,角A、B、C的对边分别为a、b、c,若
中,角A、B、C的对边分别为a、b、c,若 ,
, ,求
,求 的面积的最大值.
的面积的最大值.
试题篮
()