高中数学试题

已知圆C与直线 $x-y=0$ 及 $x-y-4=0$ 都相切，圆心在直线 $x+y=0$ 上，则圆C的方程为（ ）

A．	$(x+1{)}^2+(y-1{)}^2=2$	B．	$(x-1{)}^2+(y+1{)}^2=2$
C．	$(x-1{)}^2+(y-1{)}^2=2$	D．	$(x+1{)}^2+(y+1{)}^2=2$

已知函数 $f\left(x\right)$ 满足： $x\ge 4$ ，则 $f\left(x\right)=(\frac{1}{2}{)}^x$ ；当 $x<4$ 时 $f\left(x\right)=f(x+1)$ ，则 $f(2+{\mathit{log}}_{2}3)$ =（ ）

A．

$\frac{1}{24}$

B．

$\frac{1}{12}$

C．

$\frac{1}{8}$

D．

$\frac{3}{8}$

如果把地球看成一个球体，则地球上的北纬 $60^0$ 纬线长和赤道长的比值为（ ）

A．

0.8

B．

0.75

C．

0.5

D．

0.25

平面向量 $a$与 $b$的夹角为 $60^0$， $a=\left(2,0\right)$， $\left|b\right|=1$，则 $\left|a+2b\right|=$（ ）

A. $\sqrt{3}$    B. $2\sqrt{3}$    C.4 D.12

已知 $\left\{a_n\right\}$ 为等差数列，且 $a_7-2a_4=-1$ ， $a_3=0$ ，则公差 $d$ =（ ）

A．

-2

B．

$-\frac{1}{2}$

C．

$\frac{1}{2}$

D．

2

已知复数 $z=1-2i$ ，那么 $\frac{1}{\bar{z}}$ =（ ）

A．

$\frac{\sqrt{5}}{5}+\frac{2\sqrt{5}}{5}i$

B．

$\frac{\sqrt{5}}{5}-\frac{2\sqrt{5}}{5}i$

C．

$\frac{1}{5}+\frac{2}{5}i$

D．

$\frac{1}{5}-\frac{2}{5}i$

已知集合 $M=\left\{x\left|-3<x\right.\le 5\right\}$ , $N=\left\{x\left|x<-5或x>5\right.\right\}$ ，则 $M\cup N=$ （ ）

A．	$\left\{x\left|x<-5或x>-3\right.\right\}$	B．	$\left\{x\left|-5<x<5\right.\right\}$
C．	$\left\{x\left|-3<x<5\right.\right\}$	D．	$\left\{x\left|x<-3或x>5\right.\right\}$

（1）已知矩阵 $M\left(\begin{array}{cc}2& -3\\ 1& -1\end{array}\right)$所对应的线性变换把点 $A\left(x,y\right)$变成点 $A^{\text{'}}\left(13,5\right)$，试求M的逆矩阵及点A的坐标

（2）已知直线 $l:3x+4y-12=0$与 $圆C:\left\{\begin{array}{c}x=-1+2\mathit{cos}\theta \\ y=2+2\mathit{sin}\theta \end{array}\right.\left(\theta \mathit{为参数}\right)$试判断他们的公共点个数

（3）解不等式 $\left|2x-1\right|<\left|x\right|+1$.

已知函数 $f\left(x\right)=\frac{1}{3}{x}^3+a{x}^2+\mathit{bx}$ ,且 $f\text{'}(-1)=0$                   

(1) 试用含 $a$ 的代数式表示b,并求 $f\left(x\right)$ 的单调区间；

（2）令 $a=-1$ ,设函数 $f\left(x\right)$ 在 $x_1,x_2(x_1<x_2)$ 处取得极值，记点 $M\left(x_1,f\left(x_1\right)\right)$ ， $N\left(x_2,f\left(x_2\right)\right)$ ， $P\left(m,f\left(m\right)\right)$ , $x_1<m<x_2$ ,请仔细观察曲线 $f\left(x\right)$ 在点P处的切线与线段MP的位置变化趋势，并解释以下问题：

（Ⅰ）若对任意的 $m\in \left(x_1,x_2\right)$ ，线段MP与曲线 $f\left(x\right)$ 均有异于M,P的公共点，试确定t的最小值，并证明你的结论；

（Ⅱ）若存在点 $Q\left(n,f\left(n\right)\right)$ , $x\le n<m$ ,使得线段 $\mathit{PQ}$ 与曲线 $f\left(x\right)$ 有异于 $P$ 、 $Q$ 的公共点，请直接写出 $m$ 的取值范围（不必给出求解过程）        

已知A,B 分别为曲线C： $\frac{x^2}{a^2}+y^2=1\left(y\ge 0,a>0\right)$与x轴的左、右两个交点，直线 $l$过点B,且与 $x$轴垂直，S为 $l$上异于点B的一点，连结AS交曲线C于点T.

（1）若曲线C为半圆，点T为圆弧 $\stackrel{⏜}{\mathit{AB}}$的三等分点，试求出点S的坐标；

（2）如图，点M是以SB为直径的圆与线段TB的交点，试问：是否存在 $a$,使得O,M,S三点共线？若存在，求出 $a$的值，若不存在，请说明理由。               

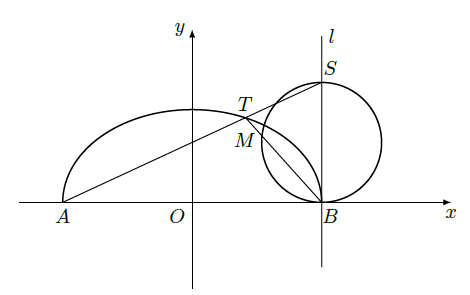
如图，某市拟在长为的道路OP的一侧修建一条运动赛道，赛道的前一部分为曲线段 $\mathit{OSM}$ ，该曲线段为函数 $y=A\mathit{sin}\omega x\left(A>0,\omega >0\right)$ ， $x\in \left[0,4\right]$ 的图象，且图象的最高点为 $S\left(3,2\sqrt{3}\right)$ ；赛道的后一部分为折线段 $\mathit{MNP}$ ，为保证参赛运动员的安全，限定 $\angle \mathit{MNP}=120°$

（Ⅰ）求A , $\omega$ 的值和M，P两点间的距离；

（Ⅱ）应如何设计，才能使折线段赛道 $\mathit{MNP}$ 最长？                                          

如图，四边形 $\mathit{ABCD}$ 是边长为 $1$ 的正方形， $\mathit{MD}\perp \mathit{平面}\mathit{ABCD}$ ， $\mathit{NB}\perp \mathit{平面}\mathit{ABCD}$ ，且 $\mathit{MD}=\mathit{NB}=1$ ， $E$ 为 $\mathit{BC}$ 的中点.

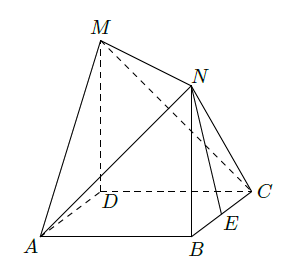
（1）求异面直线NE与AM所成角的余弦值

（2）在线段AN上是否存在点S，使得 $\mathit{ES}\perp \mathit{平面}\mathit{AMN}$ ？若存在，求线段AS的长；若不存在，请说明理由                       

从集合 $\left\{1,2,3,4,5\right\}$的所有非空子集中，等可能地取出一个。

（1）记性质r：集合中的所有元素之和为10，求所取出的非空子集满足性质r的概率；

（2）记所取出的非空子集的元素个数为 $\xi$，求 $\xi$的分布列和数学期望 $\mathit{E\xi }$

五位同学围成一圈依序循环报数，规定：

①第一位同学首次报出的数为1，第二位同学首次报出的数也为1，之后每位同学所报出的数都是前两位同学所报出的数之和；

②若报出的数为3的倍数，则报该数的同学需拍手一次

已知甲同学第一个报数，当五位同学依序循环报到第100个数时，甲同学拍手的总次数为________.

若曲线 $f\left(x\right)=a{x}^3+\mathit{ln}x$存在垂直于 $y$轴的切线，则实数 $a$取值范围是_____________.