高中物理解答题

某同学在学习了DIS实验后，设计了一个测量物体瞬时速度的实验，其装置如图所示．在小车上固定挡光片，使挡光片的前端与车头齐平、将光电门传感器固定在轨道侧面，垫高轨道的一端．该同学将小车从该端同一位置由静止释放，获得了如下几组实验数据．
实验
次数   不同的
挡光片   通过光电门的时间
（s）   速度
（m/s）
第一次    I    0.23044    0.347
第二次   Ⅱ    0.17464    0.344
第三次   Ⅲ    0.11662    0.343
第四次   Ⅳ    0.05850    0.342
（1）则以下表述正确的是   
①四个挡光片中，挡光片I的宽度最小
②四个挡光片中，挡光片Ⅳ的宽度最小
③四次实验中，第一次实验测得的速度最接近小车车头到达光电门时的瞬时速度
④四次实验中，第四次实验测得的速度最接近小车车头到达光电门时的瞬时速度
A.①③B.②③C.①④D.②④
（2）这种方法得到的测量值跟实际值相比    
A.偏大   B.偏小   C.相等
（3）若把挡光片装在小车的正中间，测量小车正中间到达光电门时的瞬时速度，测量值跟实际值相比    
A.偏大   B.偏小   C.相等．

黑体辐射的规律不能用经典电磁学理论来解释，1900年德国物理学家普朗克认为能量是由一份一份不可分割最小能量值组成，每一份称为能量子ε=hν．
1905年爱因斯坦从此得到启发，提出了光子说并成功解释了光电现象中有关极限频率、最大初动能等规律，并因此获得诺贝尔物理学奖．请写出爱因斯坦光电效应方程：      ；
1913年玻尔又受以上两位科学家的启发，把量子理论应用到原子结构中，假设了电子轨道及原子的能量是量子化的，并假定了能级跃迁时的频率条件，成功地解释了氢原子光谱的实验规律．请写出电子从高能定态（能量记为E_m）跃迁至低能态（能量记为E_n）时的频率条件方程：        ．

光滑水平面上有质量为M、高度为h的光滑斜面体A，斜面顶端放有质量为m的小物体B，A、B都处于静止状态从某时刻开始释放物体B，在B沿斜面下滑的同时斜面体A沿水平方向向左做匀加速运动．经过时间t，斜面体水平移动s，小物体B刚好滑到底端．

（1）求运动过程中斜面体A所受合力F_A的大小；
（2）分析小物体B做何种运动？并说明理由；
（3）求小物体B到达斜面体A底端时的速度v_B大小．

黑体辐射的规律不能用经典电磁学理论来解释，1900年德国物理学家普朗克认为能量是由一份一份不可分割最小能量值组成，每一份称为能量子ε=hν．
1905年爱因斯坦从此得到启发，提出了光子说并成功解释了光电现象中有关极限频率、最大初动能等规律，并因此获得诺贝尔物理学奖．请写出爱因斯坦光电效应方程：     ；
1913年玻尔又受以上两位科学家的启发，把量子理论应用到原子结构中，假设了电子轨道及原子的能量是量子化的，并假定了能级跃迁时的频率条件，成功地解释了氢原子光谱的实验规律．请写出电子从高能定态（能量记为E_m）跃迁至低能态（能量记为E_n）时的频率条件方程：    ．

黑体辐射的规律不能用经典电磁学理论来解释，1900年德国物理学家普朗克认为能量是由一份一份不可分割最小能量值组成，每一份称为能量子ε=hν．1905年爱因斯坦从此得到启发，提出了光子说并成功解释了光电现象中有关极限频率、最大初动能等规律，并因此获得诺贝尔物理学奖．请写出爱因斯坦光电效应方程：        ；1913年玻尔又受以上两位科学家的启发，把量子理论应用到原子结构中，假设了电子轨道及原子的能量是量子化的，并假定了能级跃迁时的频率条件，成功地解释了氢原子光谱的实验规律．请写出电子从高能定态（能量记为E_m）跃迁至低能态（能量记为E_n）时的频率条件方程：          ．

根据现代天文知识，恒星演化到最后可成为    或     或   ．

广义相对论认为，在任何参考系中，物理规律都是    ．

同步加速器在粒子物理研究中有重要的应用，其基本原理简化为如图所示的模型。、为两块中心开有小孔的平行金属板。质量为、电荷量为的粒子（不计重力）从板小孔飘入板间，初速度可视为零，每当进入板间，两板的电势差变为，粒子得到加速，当离开板时，两板的电荷量均立即变为零。两板外部存在垂直纸面向里的匀强磁场，在磁场作用下做半径为的圆周运动，远大于板间距离，经电场多次加速，动能不断增大，为使保持不变，磁场必须相应地变化。不计粒子加速时间及其做圆周运动产生的电磁辐射，不考虑磁场变化对粒子速度的影响及相对论效应。求

（1）运动第1周时磁场的磁感应强度的大小；

（2）在运动第n周的时间内电场力做功的平均功率；

（3）若有一个质量也为、电荷量为（k为大于1的整数）的粒子（不计重力）与A同时从板小孔飘入板间，、B初速度均可视为零，不计两者间的相互作用，除此之外，其他条件均不变，下图中虚线、实线分别表示、的运动轨迹。在的轨迹半径远大于板间距离的前提下，请指出哪个图能定性地反映、的运动轨迹，并经推导说明理由。

冰球运动员甲的质量为80.0。当他以5.0的速度向前运动时，与另一质量为100、速度为3.0的迎面而来的运动员乙相撞。碰后甲恰好静止。假设碰撞时间极短，求：
（1）碰后乙的速度的大小；

（2）碰撞中总机械能的损失。

如图所示，将小砝码置于桌面上的薄纸板上，用水平向右的拉力将纸板迅速抽出，砝码的移动很小，几乎观察不到，这就是大家熟悉的惯性演示实验。若砝码和纸板的质量分别为和，各接触面间的动摩擦因数均为。重力加速度为。

（1）当纸板相对砝码运动时，求纸板所受摩擦力大小；

（2）要使纸板相对砝码运动，求所需拉力的大小；

（3）本实验中，，，，砝码与纸板左端的距离，取。若砝码移动的距离超过，人眼就能感知，为确保实验成功，纸板所需的拉力至少多大?

如图所示，一定质量的理想气体从状态依次经过状态、和后再回到状态。其中，和为等温过程，和为绝热过程（气体与外界无热量交换）。这就是著名的"卡诺循环"。

（1）该循环过程中，下列说法正确的是.
A．过程中，外界对气体做功
B．过程中，气体分子的平均动能增大
C．过程中，单位时间内碰撞单位面积器壁的分子数增多
D．过程中，气体分子的速率分布曲线不发生变化
（2）该循环过程中，内能减小的过程是（选填""、""、""或""）. 若气体在过程中吸收的热量，在过程中放出的热量，则气体完成一次循环对外做的功为.

（3）若该循环过程中的气体为，气体在状态时的体积为，在状态时压强为状态时的。求气体在状态时单位体积内的分子数。（已知阿伏加德罗常数，计算结果保留一位有效数字）

对于同一物理问题，常常可以从宏观与微观两个不同角度进行研究，找出其内在联系，从而更加深刻地理解其物理本质。
（1）一段横截面积为、长为的直导线，单位体积内有个自由电子，电子电荷量为。该导线通有电流时，假设自由电子定向移动的速率均为。
（a）求导线中的电流；

（b）将该导线放在匀强磁场中，电流方向垂直于磁感应强度，导线所受安培力大小为，导线内自由电子所受洛伦兹力大小的总和为，推导。

（2）正方体密闭容器中有大量运动粒子，每个粒子质量为，单位体积内粒子数量为恒量。为简化问题，我们假定：粒子大小可以忽略；其速率均为，且与器壁各面碰撞的机会均等；与器壁碰撞前后瞬间，粒子速度方向都与器壁垂直，且速率不变。利用所学力学知识，导出器壁单位面积所受粒子压力与、和的关系。

（注意：解题过程中需要用到、但题目没有给出的物理量，要在解题时做必要的说明）

如图，质量为M的足够长金属导轨放在光滑的绝缘水平面上。一电阻不计，质量为的导体棒放置在导轨上，始终与导轨接触良好，构成矩形。棒与导轨间动摩擦因数为，棒左侧有两个固定于水平面的立柱。导轨段长为，开始时左侧导轨的总电阻为，右侧导轨单位长度的电阻为。以为界，其左侧匀强磁场方向竖直向上，右侧匀强磁场水平向左，磁感应强度大小均为。在=0时，一水平向左的拉力F垂直作用在导轨的边上，使导轨由静止开始做匀加速直线运动，加速度为。

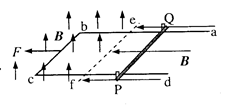
（1）求回路中感应电动势及感应电流随时间变化的表达式；
（2）经过多长时间拉力F达到最大值，拉力F的最大值为多少？
（3）某过程中回路产生的焦耳热为，导轨克服摩擦力做功为W，求导轨动能的增加量。

图所示为一种摆式摩擦因数测量仪，可测量轮胎与地面间动摩擦因数，基主要部件有：底部固定有轮胎橡胶片的摆锤和连接摆锤的轻质细杆。摆锤的质量为，细杆可绕轴在竖直平面内自由转动，摆锤重心到点距离为。测量时，测量仪固定于水平地面，将摆锤从与等高的位置处静止释放。摆锤到最低点附近时，橡胶片紧压地面擦过一小段距离，之后继续摆至与竖直方向成角的最高位置。若摆锤对地面的压力可视为大小为的恒力，重力加速度为，求

（1）摆锤在上述过程中损失的机械能；

（2）在上述过程中摩擦力对摆锤所做的功；

（3）橡胶片与地面之间的动摩擦因数。

为了提高自行车夜间行驶的安全性，小明同学设计了一种"闪烁"装置，如图所示，自行车后轮由半径的金属内圈、半径的金属内圈和绝缘辐条构成。后轮的内、外圈之间等间隔地接有4根金属条，每根金属条的中间均串联有一电阻值为R的小灯泡。在支架上装有磁铁，形成了磁感应强度、方向垂直纸面向外的"扇形"匀强磁场，其内半径为、外半径为、张角。后轮以角速度ω="2π" rad/s相对于转轴转动。若不计其它电阻，忽略磁场的边缘效应。

（1）当金属条进入"扇形" 磁场时，求感应电动势，并指出上的电流方向；

（2）当金属条进入"扇形" 磁场时，画出"闪烁"装置的电路图；

（3）从金属条进入"扇形" 磁场开始，经计算画出轮子转一圈过程中，内圈与外圈之间电势差图象；

（4）若选择的是""的小灯泡，该"闪烁"装置能否正常工作？有同学提出，通过改变磁感应强度、后轮外圈半径、角速度和张角等物理量的大小，优化前同学的设计方案，请给出你的评价。