初中数学计算器—基础知识试题

已知动点P以每秒2cm的速度沿如图所示的边框按从B⇒C⇒D⇒E⇒F⇒A的路径移动，相应的△ABP的面积S关于时间t的函数图象如图所示，若AB=6cm，试回答下列问题：
（1）动点P在线段                上运动的过程中△ABP的面积S保持不变．
（2）BC=      cm;  CD=      cm;   DE=      cm;   EF=      cm
（3）求出图乙中的a与b的值．

已知等腰三角形的周长为24cm,腰长为x(cm),底边为y(cm),则底边y与x的函数关系式为         ，自变量x的取值范围是                    ．

一艘轮船在同一航线上往返于甲、乙两地．已知轮船在静水中的速度为，水流 速度为．轮船先从甲地顺水航行到乙地，在乙地停留一段时间后，又从乙地逆水航行返回到甲地．设轮船从甲地出发后所用时间为，航行的路程为 ，则与的函数图像大致是 （       ）

一列快车从甲地驶往乙地，一列特快车从乙地驶往甲地，快车的速度为100千米/小时，特快车的速度为150千米/小时，甲乙两地之间的距离为1000千米，两车同时出发，则图中折线大致表示两车之间的距离y（千米）与快车行驶时间（小时）之间的函数图象是（　　）

A．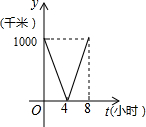

B．

C．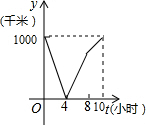

D．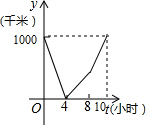

下列四幅图象近似刻画两个变量之间的关系，请按图象顺序将下面四种情景与之对应排序（　　）.

①一辆汽车在公路上匀速行驶（汽车行驶的路程与时间的关系）
②向锥形瓶中匀速注水（水面的高度与注水时间的关系）
③将常温下的温度计插入一杯热水中（温度计的读数与时间的关系）
④一杯越来越凉的水（水温与时间的关系）

A．①②④③	B．③④②①
C．①④②③	D．③②④①

下面在平面直角坐标系中所给的四个图像中，是函数图象的是(    )．

如图，在矩形ABCD中，O是对角线AC的中点，动点P从点C出发，沿DC方向匀速运动到终点C．已知P，Q两点同时出发，并同时到达终点，连接OP，OQ．设运动时间为t，四边形OPCQ的面积为S，那么下列图象能大致刻画S与t之间的关系的是

A．      B．      C．      D．

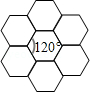
如图，蜂巢的横截面由正六边形组成，且能无限无缝隙拼接，称横截面图形由全等正多边形组成，且能无限无缝隙拼接的多边形具有同形结构．
若已知具有同形结构的正 $n$边形的每个内角度数为 $\alpha$，满足： $360=k\alpha$（ $k$为正整数），多边形外角和为360°，则 $k$关于边数n的函数是 $n$（写出 $n$的取值范围）

如图所示：边长分别为1和2的两个正方形，其中一边在同一水平线上，小正方形沿该水平线自左向右匀速穿过大正方形，设穿过的时间为t，大正方形内去掉小正方形后的面积为s，那么s与t的大致图象应为

A．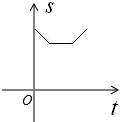

B．

C．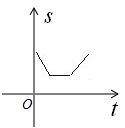

D．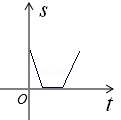

方程的根可视为函数的图象与函数的图象交点的横坐标，则方程的实根x₀所在的范围是

A．

B．

C．

D．

如图，在平面直角坐标系中，已知△ABC三个顶点的坐标分别为A（﹣1，2），B（﹣3，4）C（﹣2，6）

（1）画出△ABC绕点A顺时针旋转90°后得到的△A₁B₁C₁
（2）以原点O为位似中心，画出将△A₁B₁C₁三条边放大为原来的2倍后的△A₂B₂C₂．

已知点A（0，0），B（0，4），C（3，t+4），D（3，t）. 记N（t）为ABCD内部（不含边界）整点的个数，其中整点是指横坐标和纵坐标都是整数的点，则N（t）所有可能的值为

A．6、7

B．7、8

C．6、7、8

D．6、8、9

在平面直角坐标系xOy中，已知点A（0，1），B（1，2），点P在x轴上运动，当点P到A、B两点距离之差的绝对值最大时，点P的坐标是　   　．

在平面直角坐标系xOy中，已知A（－1，5），B（4，2），C（－1，0）三点。
（1）点A关于原点O的对称点A′的坐标为     ，点B关于x轴对称点B′的坐标为     ，点C关于y轴对称点C′的坐标为     ；
（2）求（1）中的△A′B′C′的面积。

如图，Rt△ABO的顶点A是双曲线y=与直线y=-x-（k+1）在第二象限的交点.AB⊥x轴于B，且.

（1）求这两个函数的解析式；
（2）求直线与双曲线的两个交点A、C的坐标和△AOC的面积.并根据图像写出；
（3）方程的解；
（4）使一次函数的值大于反比例函数的值的的取值范围；