如图1,已知直线 与y轴交于点A,抛物线
与y轴交于点A,抛物线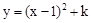 经过点A,其顶点为B,另一抛物线
经过点A,其顶点为B,另一抛物线 的顶点为D,两抛物线相交于点C
的顶点为D,两抛物线相交于点C
(1)求点B的坐标,并说明点D在直线 的理由;
的理由;
(2)设交点C的横坐标为m
①交点C的纵坐标可以表示为: 或 ,由此请进一步探究m关于h的函数关系式;
②如图2,若 ,求m的值
,求m的值
某单位准备印制一批证书,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分,乙厂直接按印刷数量收取印刷费.甲、乙两厂的印刷费用y(千元)与证书数量x(千个)的函数关系图象分别如图中甲、乙所示.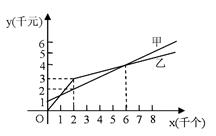
(1) 请你直接写出甲厂的制版费及y甲与x的函数解析式,并求出其证书印刷单价.
(2) 当印制证书8千个时,应选择哪个印刷厂节省费用,节省费用多少元?
 (3) 如果甲厂想把8千个证书的印制工作承揽下来,在不降低制版费的前提下,每个证书最少降低多少元?
(3) 如果甲厂想把8千个证书的印制工作承揽下来,在不降低制版费的前提下,每个证书最少降低多少元?
(本小题满分8分)北京时间2015年04月25日14时11分,尼泊尔发生8.1级强烈地震,我国积极组织抢险队赴地震灾区参与抢险工作.如图,某探测队在地面A、B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置C的深度.(结果精确到1米.参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5, ≈1.7)
≈1.7)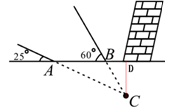
如图,在东西方向的海岸线MN上有相距10海里的A、B两艘船,均收到已触礁搁浅的船P的求救信号,已知船P在船A的北偏东60°方向上,船P在船B的北偏西45°方向上.求船P到海岸线MN的距离(结果保留根号).
如图,函数 的图象与函数
的图象与函数 (x>0)的图象交于A(a,1)、B(1,b)两点.
(x>0)的图象交于A(a,1)、B(1,b)两点.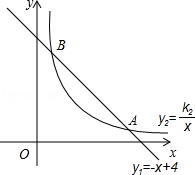
(1)求函数y2的表达式;
(2)观察图象,比较当x>0时,y1与y2的大小.
已知矩形周长为20,其中一条边长为x,设矩形面积为y
(1)写出y与x的函数关系式;
(2)求自变量x的取值范围.
某医药研究所开发了一种新药,在试验药效时发现,假如成人按规定剂量服用,那么服药后2小时时血液中含药量最高,达每毫升6微克,接着逐步衰减,10小时时血液中含药量为每毫升3微克,每毫升血液中含药量y微克随时间x小时的变化如图所示,当成人按规定剂量服药后,
(1)分别求出 x≤2和 x≥2时,y 与x之间的函数关系式
(2)假如每毫升血液中含药量为4微克或4微克以上时在治疗疾病时是有效的,那么这个有效时间是多长?
如图,根据要求回答下列问题:
(1)点A关于y轴对称点A'的坐标是____________;
点B关于y轴对称点B'的坐标是______________;
点C关于y轴对称点C'的坐标是______________;
(2)作出与△ABC关于y轴对称的图形△A′B′C′(不要求写作法)
如图①,在等腰直角三角板ABC中,斜边BC为2个单位长度,现把这块三角板在平面直角坐标系xOy中滑动,并使B、C两点始终分别位于y轴、x轴的正半轴上,直角顶点A与原点O位于BC两侧。
(1) 取BC中点D,问OD+DA是否发生改变,若会,说明理由;若不会,求出OD+DA;(2分。)
(2) 你认为OA的长度是否会发生变化?若变化,那么OA最长是多少?OA最长时四边形OBAC是怎样的四边形?并说明理由;(4分。)
(3) 填空:当OA最长时A的坐标*( , ),直线OA的解析式 。(2分。)

图① 图②备用
血橙以果肉酷似鲜血的颜色而得名,它本质上属脐橙类,现在已经开发出多种品种,果实一般在1月下旬成熟。由于果农在生产实践中积累了丰富的管理经验,大多采取了留树保鲜技术措施,将鲜果供应期拉长到了5月初。重庆市万州区晚熟柑橘以血橙为主,其中沙河街孙家村是万州血橙老产区,主要销售市场是成都、重庆市区、万州城区。据以往经验,孙家村上半年1~5月血橙的售价 (元/千克)与月份
(元/千克)与月份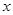 之间满足一次函数关系
之间满足一次函数关系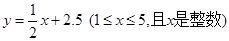 。其月销售量
。其月销售量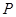 (千克)与月份
(千克)与月份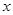 之间的相关数据如下表:
之间的相关数据如下表:
月份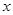 |
1月 |
2月 |
3月 |
4月 |
5月 |
销售量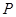 (千克) (千克) |
70000 |
65000 |
60000 |
55000 |
50000 |
请观察题中的表格,用所学过的一次函数,反比例函数或二次函数的有关知识,求月销售量
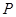 (千克)与月份
(千克)与月份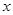 之间的函数关系式
之间的函数关系式血橙在上半年1~5月的哪个月出售,可使销售金额
 (元)最大?最大金额是多少元?
(元)最大?最大金额是多少元?由于气候适宜以及保鲜技术的提高,预计该产区今年5月将收获60000千克的血橙,并按(2)问中获得最大销售金额时的销售量售出新鲜血橙。剩下的血橙的果肉与石榴、白糖按5:2:1的比例制成“石榴·血橙白茶果冻”出售(以下简称“果冻”,制作过程中的损耗忽略不计),已知平均每千克的血橙含0.8千克的果肉。产区生产商最初将每千克果冻的批发价定为26元,超市的零售价比批发价高
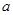 %,当销售了这批果冻的四分之三后,考虑到制作和营运成本的提高,生产商将批发价提高了
%,当销售了这批果冻的四分之三后,考虑到制作和营运成本的提高,生产商将批发价提高了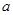 %,超市的零售价也跟着在此批发价的基础上提高了
%,超市的零售价也跟着在此批发价的基础上提高了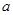 %,最后该产区将这批果冻在超市全部出售后的销售总额达到了390000元。求
%,最后该产区将这批果冻在超市全部出售后的销售总额达到了390000元。求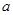 的值。(结果保留整数)
的值。(结果保留整数)
(参考数据: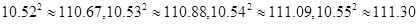 )
)
已知正比例函数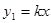 (k≠0)和反比例函数
(k≠0)和反比例函数 的图象都经过点(-2,1).
的图象都经过点(-2,1).求这两个函数的表达式;
试说明当x为何值时,

热气球的探测器显示,从热气球底部A处看一栋高楼顶部的俯角为30°,看这栋楼底部的俯角为60°,热气球A处于地面距离为420米,求这栋楼的高度.
如图,某校数学兴趣小组为测得大厦AB的高度,在大厦前的平地上选择一点C,测得大厦顶端A的仰角为30°,再向大厦方向前进80米,到达点D处(C、D、B三点在同一直线上),又测得大厦顶端A的仰角为45°,请你计算该大厦的高度.(精确到0.1米,参考数据: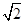 ≈1.414,
≈1.414,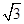 ≈1.732)
≈1.732)
试题篮
()